КАРТОГРАФИЯ
Искажения в картографических проекциях; их распределение. Определение размеров искажений на картах.
Сферическую поверхность земного шара(эллипсоида, глобуса) нельзя развернуть на плоскости карты без искажений.
В картографических проекциях могут присутствовать следующие виды искажений:
• искажения длин — вследствие этого масштаб карты непостоянен в разных точках и по разным направлениям, а длин линий и расстояния искажены;
• искажения площадей — масштаб площадей в разных точках карты различен, что является прямым следствием искажений длин и нарушает размеры объектов;
• искажения углов — углы между направлениями на карте искажены относительно тех же углов на местности;
• искажения форм — фигуры на карте деформированы и не подобны фигурам на местности, что прямо связано с искажениями углов.
Любая
бесконечно малая окружность на шаре
(эллипсоиде) предстает на карте бесконечно
малым эллипсом — его называют эллипсом
искажений.
Для
наглядности вместо бесконечно малого
эллипса обычно рассматривают эллипс
конечных размеров. Его размеры и форма
отражают искажения длин, площадей и
углов, а ориентировка большой оси
относительно меридиана и параллели —
направление наибольшего растяжения.
Большая ось эллипса искажений
характеризует направление наибольшего
растяжения в данной точке, а малая ось
— направление наибольшего сжатия,
отрезки вдоль меридиана и параллели —
соответственно характеризуют частные
масштабы по меридиану (m)
и
параллели (n).
Определив значения m
и
n,
а
также измерив угол (
),
под которым пересекаются на карте
меридиан и параллель, можно затем
рассчитать значения наибольшего (а)
и
наименьшего (ь)
частных
масштабов длин, частный масштаб площадей
(р)
в
данной точке, а также величину искажения
углов
по формулам:
р
= mn sin
Ɵ ;
a
+ b =
;
а-Ь
=
;
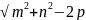sin
=
;
Если главные оси эллипса ориентированы по меридиану и параллели, то а = n и b = m либо а = m и b = n, p = mn;
sin
=
;
Значения m,n,а,Ь
и р измеряют
в процентах или в долях главного
масштаба.
Иногда в качестве показателей искажений используют величины их отклонений от единицы: m — 1 ;n — 1; а — 1; b — 1 и р — 1 — эти показатели называют относительными искажениями. Если, например, а — 1 = 0,12, то это значит, что частный масштаб вдоль большой оси эллипса искажений преувеличен относительно главного масштаба на 0,12 (или на 12%). Точно так же частный масштаб может оказаться меньше главного, например, b = 0,85 (85%), т.е. масштаб преуменьшен на 0,15 (на 15%).
В ряде проекций существуют линии и точки, где искажения отсутствуют и сохраняется главный масштаб карты, — это линии и точки нулевых искажений. Для наиболее употребительных проекций существуют специальные вспомогательные карты, на которых показаны эти линии и точки, а кроме того, проведены изоколы — линии равных искажений длин, площадей, углов или форм. При определении размеров искажений в заданной точке можно воспользоваться картами изокол либо провести несложные измерения, а затем — вычисления по приведенным выше формулам.