20. Явление электромагнитной индукции. Опыты Фарадея. Правило Ленца. Закон электромагнитной индукции по Фарадею.

в замкнутом проводящем контуре при изменении магнитного поля возникает электрический ток. Этот ток назвали индукционным током.    Индукционный ток в катушке из металлической проволоки возникает при вдвигании магнита внутрь катушки и при выдвигании магнита из катушки (рис. 192),

Явление возникновения электрического тока в замкнутом проводящем контуре при изменениях магнитного поля, пронизывающего контур, называется электромагнитной индукцией.    Появление электрического тока в замкнутом контуре при изменениях магнитного поля, пронизывающего контур, свидетельствует о действии в контуре сторонних сил неэлектростатической природы или о возникновении ЭДС индукции.   

Правило Ленца. Опыт показывает, что направление индукционного тока в контуре зависит от того, возрастает или убывает магнитный поток, пронизывающий контур, а также от направления вектора индукции магнитного поля относительно контура. Общее правило, позволяющее определить направление индукционного тока в контуре, было установлено в 1833 г. Э. X. Ленцем.          Общая формулировка правила Ленца: возникающий в замкнутом контуре индукционный ток имеет такое направление, что созданный им магнитный поток через площадь, ограниченную контуром, стремится компенсировать то изменение магнитного потока, которым вызывается данный ток.     ЭДС индукции в замкнутом контуре пропорциональна скорости изменения магнитного потока через поверхность, ограниченную контуром.    С учетом правила Ленца закон электромагнитной индукции записывается следующим образом: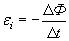 .(54.3)

   

 

21. Индуктивность. Явление самоиндукции. Токи при замыкании и размыкании цепи.

Между величиной тока в проводнике и величиной магнитного поля (магнитного потока Ф) существует прямая зависимость: - индуктивность проводника L - коэффициент пропорциональности между Ф и I. Индуктивность L зависит от свойств самого проводника (его формы, размеров, количества витков и т.п., а также магнитной проницаемости среды μ). Так магнитное поле катушки (соленоида) много сильнее магнитного поля прямого проводника при прочих равных условиях. L не зависит от силы тока I, магнитного поля Ф и т.п. Формулы, где встречается L: 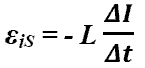 - ЭДС самоиндукции при изменении тока в проводнике. 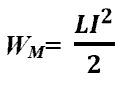 - энергия магнитного поля катушки с током. - формула Томсона для периода электромагнитных колебаний в колебательном контуре LC.

. Явление возникновения ЭДС в цепи вследствие изменения силы тока в этой же цепи называется самоиндукцией. Это явление является частным случаем электромагнитной индукции, поэтому формула для ЭДС самоиндукции остается прежней

где Ф − магнитный поток поля, создаваемого током в контуре. В соответствии с правилом Ленца возможный индукционный ток препятствует изменению магнитного потока через контур. Поэтому ЭДС самоиндукции препятствует изменению тока в цепи.

 

 

 

22. Энергия проводника и системы проводников с током. Объемная плотность энергии магнитного поля.

Энергия магнитного поля. Плотность энергии.

В опыте, схема которого приведена на рис.14.7, после размыкания ключа через гальванометр некоторое время течет убывающий ток. Работа этого тока равна работе сторонних сил, роль которых выполняет ЭДС самоиндукции 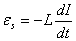 , действующая в контуре. Пусть за время dt по цепи переносится заряд dq. Работа тока самоиндукции по перемещению этого заряда есть:

.

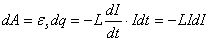Проинтегрировав это выражение в пределах от I до 0, получим полную работу тока:

.

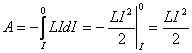Совершение этой работы сопровождается исчезновением магнитного поля, которое первоначально существовало в соленоиде и окружающем его пространстве. Остается заключить, что магнитное поле является носителем той энергии, за счет которой производится работа тока, идущая на изменение внутренней энергии проводников – их нагревание.

Выразим эту энергию через величины, характеризующие само поле. Для этого заменим индуктивность соленоида ее выражением 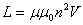 . Далее, замечая, что напряженность магнитного поля соленоида  , приходим к формуле: 

.

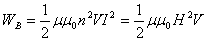Полученному выражению для энергии магнитного поля можно придать другой вид, если учесть, что  :

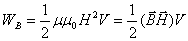
Плотность энергии магнитного поля получим, поделив это выражение на объем V, занятый полем: