18. Действие магнитного поля на движущийся заряд. Сила Лоренца. Движение заряженных частиц в магнитном поле.

Выражение для силы F, действующей на заряд q , движущийся в магнитном поле B, было получено Г. Лоренцом, эта сила называется силой Лоренца F_л = q [ v, B] Численное значение силы Лоренца равно F_л = q v B sin α, где α – угол между векторами v и B. Сила Лоренца всегда направлена перпендикулярно к скорости движения заряда и поэтому играет роль центростремительной силы. Следовательно, сила Лоренца не совершает работы. Она изменяет только направление скорости движения заряда в магнитном поле. Абсолютная величина скорости заряда и его кинетическая энергия при движении в магнитном поле не изменяются.

. Ускорители заряжен­ных частиц— устройства для получения заряженных частиц (электронов, протонов, атомных ядер, ионов) больших энергий. Ускорение производится с помощью электрического поля, способного изменять энергию частиц, обладающих электрическим зарядом. Магнитное поле может лишь изменить направление движения заряженных частиц, не меняя величины их скорости, поэтому в ускорителях оно применяется для управления движением частиц (формой траектории). Обычно ускоряющее электрическое поле создаётся внеш­ними устройствами (генераторами).

19. Магнитный поток. Теорема Остроградского-Гаусса для магнитного поля. Работа перемещения проводника с током в магнитном поле.

Магнитный поток. Работа по перемещению проводника и контура с током в магнитном поле

Основные формулы

      Магнитный момент замкнутого плоского контура, обтекаемого током  ,

,                                                  (12)

где  – площадь, ограниченная контуром;  – единичный вектор нормали к плоскости контура.

      Поток вектора магнитной индукции  (магнитный поток) сквозь поверхность S

,                                      (13)

где    – вектор, численно равный элементу площади  , направление которого совпадает с положительным направлением нормали к плоскости контура;   – проекция вектора  на направление нормали   к площадке  ;   – угол между векторами  и  .

      Поток вектора магнитной индукции (магнитный поток) сквозь площадку 

.                                       (14)

где  – вектор, модуль которого равен  , а направление совпадает с направлением нормали   к площадке.

       Магнитный поток сквозь плоскую поверхность  , находящуюся в однородном поле,

.                                                 (15)

        Поток вектора магнитной индукции сквозь соленоид

 

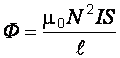,                                            (16)

где  – магнитная постоянная;  – число витков соленоида;  – площадь витков соленоида;  – сила тока.

      Элементарная работа по перемещению  проводника с током в магнитном поле

,                                (17)

где    – угол между векторами  и .

 

. Поток вектора магнитной индукции. Теорема Гаусса для магнитного поля. 

. Магнитное поле создается в пространстве вокруг движущихся электрических зарядов или постоянных токов. Основной характеристикой магнитного поля является вектор магнитной индукции В. Условились считать, что вектор магнитной индукции В в произвольной точке поля совпадает по направлению с силой, действующей на северный полюс бесконечно малой магнитной стрелки, помещенной в эту точку поля.. Направление линий индукции магнитного поля тока определяется по известному правилу правого винта (или буравчика): если ввинчивать буравчик по направлению движения тока в проводнике, то направление движения его рукоятки укажет направление линий магнитной индукции. Поток вектора В, как и любого другого, определяется выражением dФ_В = B dS = B_n dS Если поле однородное, а поверхность S плоская и расположена перпендикулярно вектору В, то B_n = В = const, то Ф_В = B S. Замкнутость линий вектора В определяет и свойства его потока. Пусть какая-то поверхность натянута на контур (как мыльная пленка на проволочное кольцо). Поток вектора В не зависит от формы этой поверхности, так как поток определяется только числом линий, прохо­дящих внутри контура. Количество силовых линий, входящих и выходящих из этой замкнутой поверхности, одинаково. Следовательно, Ф_В =   В dS = 0. Эта формула выра­жает теорему Гаусса для магнитного поля: поток вектора В сквозь любую замкнутую поверхность всегда равен нулю.