16. Закон Био-Савара-Лапласа и его применение к расчету магнитного поля кругового тока. Магнитный момент витка с током.

Закон Био- Савара – Лапласа связывает элементарный (малый) участок тока с индукцией магнитного поля, которую этот участок создает. Закон Био- Савара – Лапласа : элемент тока dl , по которому течет ток I , создает в вакууме в произвольно выбранной точке А (рис) магнитное поле, индукция которого , dB равна dB = , где r – расстояние от элемента тока dl до точки А, α – угол, который радиус вектор r, проведен­ный к точке А составляет с элементом dl, μ₀ = 4π · 10^-7 Гн/м – магнитная постоянная. В векторном виде формулу (12.1) можно представить как dB = Найдем индукцию В в центре кругового тока радиуса R, рис. Любой элемент dl создает в центре О индукцию dB, направление которой перпендикулярно плоскости контура, будем считать его направлением положительной нормали n. Так как направление векторов dB от всех элементов одинаково, то векторное сложение можно заменить алгебраическим. Согласно з-ну Б-С-Л , поскольку α = π /2, dB = , Интегрируя это выражение по контуру, получаем В = Используя принцип суперпозиции В= , получим ∫ dl = = , p_m = I S – магнитный момент контура, направленный так же как положительная нормаль n, S = π R² – площадь контура.

17. Вихревой характер магнитного поля. Закон полного тока (циркуляция вектора магнитной индукции) для магнитного поля в вакууме и его применение к расчету магнитного поля длинного соленоида.

 Вихревой характер магнитного поля. Закон полного тока. Непотенциальность магнитного поля

М 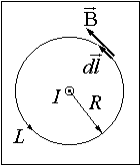агнитная индукция бесконечно длинного прямого повода с током находится по формуле (3.6.3). Проведем через точку наблюдения, отстоящую от проводя на произвольное расстояние R окружность L концентричную проводу (см рис.3.6.1, ток направлен на нас). На всей этой окружности значение   неизменно, а сам вектор B направлен по касательной к окружности (B_l = B). Поэтому циркуляция вектора B по окружности вычисляется просто:

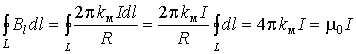.                             (3.7.1)

П ри этом под I подразумевается алгебраическая сумма этих токов. Знак плюс в этой сумме соответствует токам, направление которых связано с направлением обхода контура (т.е. выбором направления вектора   в левой части (3.7.2)) правилом буравчика (правого винта). Токи противоположного направления входят в суммарный ток, обозначенный в формуле (3.7.2) через I , со знаком минус (см. ток I₂ на рис.3.7.2). Закон полного тока в форме (3.7.2) выполняется не только для прямолинейных проводов с токами, но и для произвольных (криволинейных) токов.

Применим закон полного тока для бесконечно малой окружности площадью dS, через которую протекает бесконечно малый ток dI. Используя формулу, выражающую ток через площадку через плотность тока, т.е. dI =j dS, и выражение ротора векторного поля через циркуляцию по бесконечно малой окружности (см. формулу(1.5.3)), получим закон полного тока в дифференциальной форме:

ивергенция электростатического поля не равна нулю в области источников.

Итак, электрические токи (направленное движение заряда) создают магнитное поле, а нескомпенсированные заряды – электростатическое поле. Внутри проводника имеется электрическое поле из-за наличия ЭДС в цепи с током.