4. Поток вектора напряженности. Теорема Остроградского-Гаусса для электростатического поля в вакууме. Применение теоремы Остроградского-Гаусса к расчету поля бесконечной заряженной плоскости.

Найдем поток вектора Е сквозь сферическую поверхность S, в центре которой находится точечный заряд q. В Очевидно, что поверхность S₁ пересекается тем же числом линий Е, что и пов-ть S. Следовательно, поток вектора Е сквозь произвольную поверхность S₁ также определяется полученной формулой Ф_Е. Если за­ряд будет находится вне замкнутой пов-ти, то, очевидно, сколько линий войдет в замкнутую область, столько же из нее и выйдет. В результате поток в-ра Е будет равен нулю. Если электрическое поле создается с-мой точечных зарядов q₁, q₂, q₃,…, то согласно принципу суперпозиции, Ф_Е = =Ф_Е1+Ф_Е2+…=∑q_i /ε₀. Эта формула является мате­матическим выражением теоремы Гаусса: поток в-ра напряжен­ности Е электрического поля в вакууме через произвольную замкнутую пов-ть равен алгебраической сумме за­рядов, которые она охватывает, деленной на ε₀. Ф_Е =∑q_i /ε₀Применение теоремы Гаусса для расчета электрического поля равномерно заряженной бес­конечной плоскости.

Е_n=Е=const. Следовательно, полный поток будет равен потоку Е_n через два основания цилиндра Ф_Е =E =2ES=2Eπr². Так как заряд, находящийся внутри цилиндра, ра­вен q=σπr² то Е=σ/(2ε₀). Как следует из этой ф-лы, напряженность поля не зависит от рас­стояния до заряженной пл-ти, т.е. поле бесконечно заряженной пл-ти является однород­ным.

5. Свободные и связанные заряды. Полярные и неполярные молекулы. Поляризуемость молекулы. Типы диэлектриков. Поляризованность вещества.

свободные заряды: электроны или положи­тельно (отрицательно) заряженные ионы. Электрический диполь, хотя он электрически нейтрален, также содержит в себе отрицательный и положительный заряды. Эти заряды называются связан­ными.

Атом диэлектрика в электрическом поле. Он состоит из положительно заряженного ядра и некоторой отрицательно заряженной области, в которой движутся электроны.

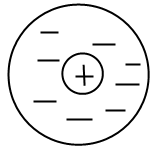
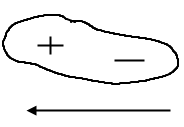
Если «центр инерции» этой области совпадает с ядром, то молекула называется неполярной (H₂, N₂, углеводороды). Если же «центр инерции» области отрицательного заряда не совпадает с ядром, то молекулу называют полярной (H₂O, HCl). положительные заряды диэлектрика смещаются по полю, а отрицательные – против поля. Это явление называют поляризацией диэлектрика. В отличие от проводника смещение зарядов в диэлектрике происходит только в пределах каждой молекулы.. Величина Р называется вектором поляризации или поляризованностью. Вектором поляризованности Р называют дипольный момент единицы объема диэлектрика, возникающий при его поляризации.

6. Теорема Остроградского-Гаусса для электрического поля в диэлектрике. Электрическое смещение. Диэлектрическая проницаемость среды.

Связанные заряды q΄ , как и свободные q , служат источником линий электрического поля. По­этому теорему Гаусса с учетом связанных зарядов следует представлять в виде = (q΄ + q) / ε_0. Пользоваться этой формулой для вычисления поля в диэлектрике не совсем удобно, т.к. в нее входят две неизвестные: Е и q΄. Для этого вводят электрическое смещение или вектор электри­ческой индукции D : D = ε₀Е + Р. Тогда вместо нее получаем теорему Гаусса для поля вектора D: = q поток вектора D сквозь замкну­тую поверхность равен сумме свобод­ных зарядов, охваченных этой поверхностью. В то же время формула по­зволяет по вектору D определить вектор Е. Подставив P=χε₀E в D = ε₀Е + Р, получим D= ε₀ ε Е, где ε = 1 + χ – диэлектрическая проницаемость ве­щества, безразмерная величина. Обобщение теоремы Гаусса на случай поля в диэлектрике: =q/ (ε₀ ε)

7. Проводники в электрическом поле. Условия равновесия зарядов. Поле внутри проводника и у его поверхности. Электростатическая защита. Распределение зарядов в проводнике. Напряженность поля вблизи поверхности заряженного проводника.

К проводникам относят вещества, у которых имеются свободные заряженные частицы, способные двигаться упорядоченно по всему объему тела под действием электрического поля. Проводниками являются металлы, некоторые химические соединения, водные растворы солей, кислот и щелочей, расплавы солей, ионизированные газы. Условия равновесия зарядов в проводниках

Если электрические заряды находятся в равновесии в каком-либо проводнике, т. е. в этом проводнике нет электрического тока, то напряженность поля E_i в любой точке внутри проводника равна

нулю.. Кроме того, при равновесии зарядов век­тор напряженности поля у поверхности проводника пер­пендикулярен к поверхности. Отсюда следует, что для пе­ремещения заряда из любой точки проводника в любую другую его точку не требует­ся никакой работы. Но разность потенциалов любой пары точек как внутри проводника, так и на поверхности равна нулю. В отсутствии электрического тока все точки проводника имеют одинаковый электрический потенциал.

Распределение зарядов в проводнике.

Все вещества в соответствии с их способностью проводить электрический ток подразделяются на проводники, диэлектрики и полупроводники. Проводниками называют вещества, в которых электрически заряженные частицы - носители заряда- способны свободно перемещаться по всему объему вещества.

Электростатическая защита

На судах в качестве топлива и смазочных масел для судовых машин и в качестве груза перевозится значительное количество материалов, являющихся диэлектриками, способными накапливать заряды статического электричества. При выполнении некоторых технологических операций на судах (перекачка топлива или сырой нефти, мойка танков и т. п.) возможно искрообразование, обусловленное разрядами статического электричества.