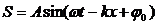- •1. Закон сохранения электрического заряда. Закон Кулона. Электрическое поле. Напряженность электрического поля. Принцип суперпозиции полей.
- •1.1. Электрический заряд. Закон сохранения заряда
- •1.2. Закон Кулона
- •1.4.Принцип суперпозиции электрических полей
- •2. Работа перемещения электрического заряда в электростатическом поле. Циркуляция вектора напряженности электрического поля.
- •3. Потенциал и разность потенциалов. Напряженность как градиент потенциала.
- •4. Поток вектора напряженности. Теорема Остроградского-Гаусса для электростатического поля в вакууме. Применение теоремы Остроградского-Гаусса к расчету поля бесконечной заряженной плоскости.
- •5. Свободные и связанные заряды. Полярные и неполярные молекулы. Поляризуемость молекулы. Типы диэлектриков. Поляризованность вещества.
- •6. Теорема Остроградского-Гаусса для электрического поля в диэлектрике. Электрическое смещение. Диэлектрическая проницаемость среды.
- •8. Электроемкость уединенного проводника. Взаимная емкость двух проводников. Конденсаторы.
- •9. Энергия заряженных уединенного проводника, конденсатора и системы проводников. Энергия электростатического поля. Объемная плотность энергии.
- •10. Постоянный электрический ток, его характеристики и условия существования. Классическая электронная теория (кэт) электропроводности металлов и ее опытное обоснование. Плотность тока по кэт.
- •11. Вывод закона Ома в дифференциальной форме из электронных представлений. Затруднения кэт.
- •12. Обобщенный закон Ома в интегральной форме. Разность потенциалов, электродвижущая сила, напряжение. Границы применимости закона Ома.
- •13Электрический ток в вакууме. Термоэлектронная эмиссия. Законы, описывающие электрический ток в вакууме. Электрический ток в вакууме.
- •Вольт-амперная характеристика вакуумного диода.
- •Вольт- амперная характеристика газов.
- •15. Магнитное поле. Магнитная индукция. Закон Ампера. Контур с током в магнитном поле.
- •16. Закон Био-Савара-Лапласа и его применение к расчету магнитного поля кругового тока. Магнитный момент витка с током.
- •18. Действие магнитного поля на движущийся заряд. Сила Лоренца. Движение заряженных частиц в магнитном поле.
- •19. Магнитный поток. Теорема Остроградского-Гаусса для магнитного поля. Работа перемещения проводника с током в магнитном поле.
- •20. Явление электромагнитной индукции. Опыты Фарадея. Правило Ленца. Закон электромагнитной индукции по Фарадею.
- •21. Индуктивность. Явление самоиндукции. Токи при замыкании и размыкании цепи.
- •22. Энергия проводника и системы проводников с током. Объемная плотность энергии магнитного поля.
- •23. Магнитное поле в веществе, микро - и макро токи. Магнитные моменты атомов. Типы магнетиков. Намагниченность.
- •24. Закон полного тока для магнитного поля в веществе. Напряженность магнитного поля. Магнитная проницаемость среды. Напряженность магнитного поля. Закон полного тока
- •25. Ферромагнетики. Опыты Столетова. Основная кривая намагничивания ферромагнетика. Магнитный гистерезис. Точка Кюри для ферромагнетика. Домены. Спиновая природа ферромагнетизма.
- •26. Основы теории Максвелла для электромагнитного поля. Ток смещения. Закон полного тока для магнитного поля по Максвеллу.
- •27. Система уравнений Максвелла в интегральной форме для электромагнитного поля.
- •28Гармонические колебания (механические и электромагнитные) и их характеристики
- •29 Дифференциальное уравнение вынужденных колебаний (механических и электромагнитных) и его решение
- •30 Пружинный, математический и физический маятники. Колебательный контур. Пружинный маятник
- •Математический маятник
- •Физический маятник
- •31 Энергия гармонических колебаний
- •32 Сложение гармонических колебаний одного направления и одинаковой частоты, условия усиления и ослабления.
- •33 Биения. Уравнение биений и его анализ.
- •34. Дифференциальное уравнение затухающих колебаний и его решение. Амплитуда и фаза собственных затухающих колебаний.
- •35. Дифференциальное уравнение вынужденных колебаний и его решение. Амплитуда и фаза вынужденных колебаний. Явление резонанса. Резонансная кривая. Резонансная частота.
- •36. Волна. Механизм образования механических волн в упругой среде. Продольные и поперечные волны. Синусоидальные (гармонические) волны. Уравнение бегущей волны. Длина волны и волновое число.
- •37. Энергия гармонической волны. Гармоническая волна. Волна, каждая точка которой, в пространстве совершает гармонические колебания.
- •38. Когерентность. Принцип суперпозиции волн. Интерференция волн. Условия усиления и ослабления.
- •39. Стоячая волна. Уравнение стоячей волны и его анализ.
- •40. Основные свойства электромагнитных волн. Монохроматическая волна.
- •]Стоячая монохроматическая волна
34. Дифференциальное уравнение затухающих колебаний и его решение. Амплитуда и фаза собственных затухающих колебаний.
Затухающие колебания — колебания, амплитуды которых из-за потерь энергии реальной колебательной системой с течением времени уменьшаются.
Дифференциальное уравнение свободных затухающих колебаний линейной системы
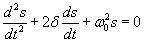
где s — колеблющаяся величина, описывающая тот или иной физический процесс, δ = const — коэффициент затухания, (ω0 — циклическая частота свободных незатухающих колебаний той же колебательной системы, т. е. при δ =0 (при отсутствии потерь энергии) называется собственной частотой колебательной системы.
Решение уравнения рассмотрим в виде
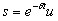 (7.1)
где u=u(t).
(7.1)
где u=u(t).
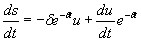
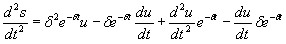
После нахождения первой и второй производных и их подстановки в (1) получим
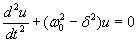
35. Дифференциальное уравнение вынужденных колебаний и его решение. Амплитуда и фаза вынужденных колебаний. Явление резонанса. Резонансная кривая. Резонансная частота.
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ - колебания, происходящие под действием внешней переменной силы (вынуждающей силы).
Установившиеся вынужденные колебания происходят с частотой, равной частоте вынуждающей силы.
В каноническом виде дифференциальное уравнение вынужденных механических колебаний имеет вид:
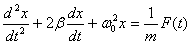
Для пружинного маятника:
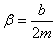 и
и 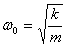
Для амплитуды и сдвига фаз получаются следующие выражения:
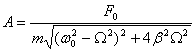
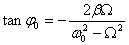
здесь - частота свободных (незатухающих) колебаний маятника; - коэффициент затухания.
Обратите
внимание, что амплитуда вынужденных
колебаний зависит от соотношения частоты
вынуждающей силы и собственной частоты
маятника. Максимальное значение амплитуды
получается, если 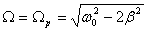
Частота ![]() называется резонансной
частотой,
а достижение максимума амплитуды
колебаний при изменении частоты
называется явлением резонанса.
называется резонансной
частотой,
а достижение максимума амплитуды
колебаний при изменении частоты
называется явлением резонанса.
36. Волна. Механизм образования механических волн в упругой среде. Продольные и поперечные волны. Синусоидальные (гармонические) волны. Уравнение бегущей волны. Длина волны и волновое число.
Волны - возмущения, распространяющиеся в пространстве с течением времени.
Процесс распространения колебаний в пространстве называется волной.
Частицы среды, в которой распространяется волна, не вовлекаются волной в поступательное движение, они лишь совершают колебания около своих положений равновесия. В зависимости от направления колебаний частиц по отношению к направлению распространения волны, различают продольные и поперечные волны.
Продольная волна – это волна, в которой частицы среды колеблются вдоль направления распространения волны.
Поперечная волна - это волна, в которой частицы среды колеблются в направлениях, перпендикулярных к направлению распространения волны.
Упругие поперечные волны могут возникать лишь в среде, обладающей сопротивлением сдвигу. Поэтому в жидкой и газообразной средах возможно возникновение только продольных волн. В твердой среде возможно возникновение как продольных, так и поперечных волн.
Уравнение плоской одномерной синусоидальной волны:
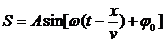
Расстояние, на которое распространяется волна за время, равное периоду колебаний, называется ДЛИНОЙ ВОЛНЫ = .
ВОЛНОВОЕ ЧИСЛО k:
![]()
С помощью введенного волнового числа уравнение волны запишется: