29 Дифференциальное уравнение вынужденных колебаний (механических и электромагнитных) и его решение

Тогда дифференциальное уравнение колебаний заряда Q в простейшем контуре, используя (3), можно записать как 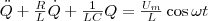   Зная формулу циклической частоты свободных колебаний колебательного контура и формулу предыдущего раздела (11), придем к дифференциальному уравнению   (4)  Колебания, которые возникают под действием внешней периодически изменяющейся силы или внешней периодически изменяющейся э.д.с., называются соответственно вынужденными механическими и вынужденными электромагнитными колебаниями.  Уравнения (2) и (4) приведем к линейному неоднородному дифференциальному уравнению   (5)  причем далее мы будем применять его решение для вынужденных колебаний в зависимости от конкретного случая (x₀ если механические колебания равно F₀/m, в случае электромагнитных колебаний - U_m/L). 

30 Пружинный, математический и физический маятники. Колебательный контур. Пружинный маятник

 Пружинный маятник — это груз массой т, подвешенный на абсолютно упругой пружине и совершающий гармонические колебания под действием упругой силы F = –kx, где k — жесткость пружины. Уравнение движения маятника

Период колебаний пружинного маятника может быть вычислен по следующей формуле:

,

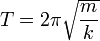где   — масса груза,   — жёсткость пружины.

Математический маятник

Математический маятник — это идеализированная система, состоящая из материальной точки массой т, подвешенной на нерастяжимой невесомой нити, и колеблющаяся под действием силы тяжести. Хорошим приближением математического маятника является небольшой тяжелый шарик, подвешенный на тонкой длинной нити

Период колебаний математического маятника:

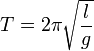
где   — длина подвеса (к примеру нити),   — ускорение свободного падения.

Период колебаний (на Земле) математического маятника длиной 1 метр с хорошей точностью^[5] равен 2 секундам.

Физический маятник

это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси, проходящей через точку О, не совпадающую с центром масс тела

Период колебаний физического маятника:

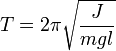
где   — момент инерции маятника относительно оси вращения,   — масса маятника,   — расстояние от оси вращения до центра масс.

Колебательный контур 

Колебательный контур — осциллятор, представляющий собой электрическую цепь, содержащую соединённые катушку индуктивности и конденсатор. В такой цепи могут возбуждаться колебания тока (и напряжения).

Колебательный контур — простейшая система, в которой могут происходить свободные электромагнитные колебания

Резонансная частота контура определяется так называемой формулой Томсона:

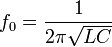
31 Энергия гармонических колебаний

        При механических колебаниях колеблющееся тело (или материальная точка) обладает кинетической и потенциальной энергией. Кинетическая энергия тела W:

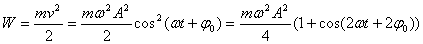
(Скорость тела v = ds/dt)

        Для вычисления потенциальной энергии тела воспользуемся самой общей формулой, связывающей силу и потенциальную энергию тела в поле этой силы:

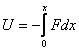
где U - потенциальная энергия, набираемая (или теряемая) телом, движущимся в силовом поле F от точки 0 (точки, в которой потенциальная энергия принимается равной 0) до точки х.

       

1. Полная механическая энергия тела не изменяется при колебаниях: 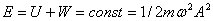   2. Частота колебаний кинетической и потенциальной энергии в 2 раза больше частоты колебаний маятника.  3. Колебания кинетической и потенциальной энергии сдвинуты друг относительно друга по фазе на  (на полпериода). Когда кинетическая энергия достигает максимума, потенциальная - минимума (нуля) и наоборот. Энергия при колебаниях постоянно перекачивается из потенциальной в кинетическую и обратно.

       

выводы:

1. Полная энергия в контуре остается неизменной: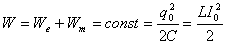 

2. Частота колебаний энергий в 2 раза превосходит частоту колебаний заряда и тока в контуре.  3. Электрическая и магнитная энергии сдвинуты по фазе на полпериода друг относительно друга; происходит непрерывное перекачивание энергии из одной формы в другую и обратно.

        Поскольку в контуре происходят колебания электрической и магнитной энергий, электрический колебательный контур также называют электромагнитным.