27. Система уравнений Максвелла в интегральной форме для электромагнитного поля.

Уравнения Максвелла для электромагнитного поля

можно представить полную систему уравнений Максвелла в дифференциальной форме (характеризующих поле в каждой точке пространства):               Если заряды и токи распределены в пространстве непрерывно, то обе формы уравнений Максвелла – интегральная и дифференциальная – эквивалентны. Однако если имеются поверхности разрыва (поверхности, на которых свойства среды или полей меняются скачкообразно), то интегральная форма уравнений является более общей. Уравнения Максвелла в дифференциальной форме предполагают, что все величины в пространстве и времени изменяются непрерывно. Чтобы достичь математической эквивалентности обеих форм уравнений Максвелла, дифференциальную форму дополняю граничными условиями, которым должно удовлетворять электромагнитное поле на границе раздела двух сред. Интегральная форма уравнений Максвелла содержит эти условия               Первое и последнее уравнение отвечают случаям, когда на границе раздела двух сред нет ни свободных зарядов, ни токов проводимости. Уравнения Максвелла – наиболее общие уравнения для электрических и магнитных полей в покоящихся средах. Они играют в учении об электромагнетизме такую же роль, как законы Ньютона в механике. Из уравнений Максвелла следует, что переменное магнитное поле всегда связано с порождаемым им электрическим полем, а переменное электрическое поле всегда связано с порождаемым им магнитным, т.е. электрическое и магнитное поля неразрывно связаны друг с другом – они образуют единое электромагнитное поле.

28Гармонические колебания (механические и электромагнитные) и их характеристики

Колебаниями называются движения или процессы, характеризующиеся определенной повторяемостью во времени. Колебательные процессы имеют широкое распространение в природе и технике, например качание маятника часов, переменный электрический ток и т. д. При колебательном движении маятника меняет свое положение координата его центра масс, при переменном токе меняют свои характеристики с определенной повторяемостью напряжение и ток в цепи. Колебательный процесс может имет различную физическую природу, поэтому различают колебания механические, электромагнитные и др. Но различные колебательные процессы характеризуются одинаковыми физическими параметрами и одинаковыми уравнениями. Отсюда вытекает целесообразность единого подхода к исследованию колебаний различной физической природы. Колебания называются свободными (или собственными), если они совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воздействий на систему, которая совершает колебания. Простейшим типом колебаний являются гармонические колебания — колебания, при которых колеблющаяся величина изменяется со временем по закону синуса (косинуса). Исследование гармонических колебаний важно по двум причинам: 1) колебания, которые встречаются в природе и технике, часто имеют близкий к гармоническому характер ; 2) различные периодические процессы (процессы, которые повторяются через равные промежутки времени) можно представить как суперпозицию (наложение) гармонических колебаний. Гармонические колебания некоторой величины s описываются уравнением вида 

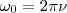
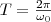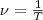  (2)  Величина, обратная периоду колебаний,    (3)  т. е. число полных колебаний, которые совершаются в единицу времени, называется частотой колебаний. Сопоставляя (2) и (3), найдем    Единица частоты — герц (Гц): 1 Гц — частота периодического процесса, во время которого за 1 с совершается один цикл процесса.