Разложение многочлена над полем действительных числе на неприводимые множители

с действительными коэффициентами.

Над полем C этот многочлен имеет n корней и разлагается на n линейных множителей.

, над C.

Некоторые могут быть действительными.

Пусть для определенности

.

- комплексные корни.

, тогда по теореме о существовании сопряженного корня среди найдется число сопряженное .

.

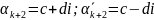Комплексных корней четное число и они попарно сопряжены

,

с действительными коэффициентами

.

. (*)

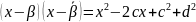- многочлены второй степени с действительными коэффициентами, корни которых комплексно-сопряженные.

Все множители разложения (*) многочлены с действительными коэффициентами.

Всякий многочлен с действительными коэффициентами над R разлагается на произведение старшего коэффициента, линейных множителей вида , соответствующих действительным корням, и квадратных множителей вида , соответствующих парам комплексно-сопряженных корней.

Следствие: Неприводимыми многочленами над P являются многочлены 1 степени и 2-ой степени, у которых D<0.

Теорема: Все многочлены выше второй степени над полем действительных чисел приводимы.

Доказательство:

Пусть с действительными коэффициентами степени . По основной теореме алгебры существует корень α, если:

1. α – действительный корень, ;

2. α - комплексный корень => у многочлена

.

.

Все многочлены выше второй степени – приводимы. Ч.т.д.

Многочлены над полем рациональных чисел

Многочлен вида

,

называется примитивным, если его коэффициенты взаимно простые числа

.

Например: - примитивный.

Теорема: Всякий многочлен с рациональными коэффициентами можно представить в виде произведения несократимой дроби на примитивный многочлен.

Доказательство:

, .

.

.

Найдется - общий знаменатель.

По свойству дробей все коэффициенты можно привести к общему знаменателю .

.

.

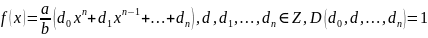- примитивный многочлен.

Если – несократимая, то теорема доказана.

Если - сократимая, то , – примитивный.

. Ч.т.д.

Например: .

.

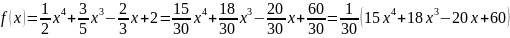Лемма Гаусса: Произведение примитивных многочленов является примитивным.

Доказательство:

.

.

.

.

Предположим, что этот многочлен не примитивный. Тогда .

- простое число, на которое все коэффициенты делятся.

.

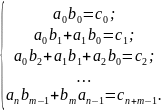
Т.к. многочлены являются примитивными, то все коэффициенты и первого, и второго многочлена делиться на p не могут.

Пусть .

.

.

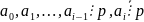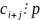по условию все слагаемые, кроме одного делятся на p. Тогда , отсюда или , а это противоречит выбору коэффициентов . Противоречие в результате неверного предположения. Значит . Значит многочлены – примитивные.

Сведение вопроса о приводимости многочленов над полем рациональных числе к вопросу о приводимости этих многочленов над кольцом целых чисел.

Пусть многочлен с рациональными коэффициентами. Тогда его можно представить как , – примитивный, – несократимая дробь.

Если с целыми коэффициентами будет приводим над Z:

, с целыми коэффициентами, ст. , ст. ,

тогда , - приводим.

Пусть приводим над Q. Тогда покажем, что он приводим над кольцом Z.

Пусть с рациональными коэффициентами.

Тогда

.

Тогда .

По лемме Гаусса 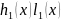– примитивные его коэффициенты целого и взаимно простые, - примитивный с целыми и взаимно простыми коэффициентами.

Тогда .

Произведение примитивно умноженного на 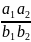даст нам многочлен с целыми коэффициентами  .

А значит .

Т.к. 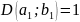, то , .

Т.к. , то .

Получили .

Разложили , приводим над Z. Значит будет приводим над Q.

Вопрос о приводимости многочлена над Q сводится к вопросу о приводимости над Z.