Формула Тейлора. Разложение многочлена по степеням линейного двучлена.

- n-ой степени.

.

.

Подставляем вместо x с.

.

Найдем .

.

.

.

.

.

.

.

.

.

, (*)

.

Чтобы найти коэффициент в формуле Тейлора надо найти сами производные, найти их значение и разделить на k!

Из (*): .

.

.

Подставляем вместо x с.

.

.

.

.

.

.

…

...

.

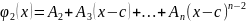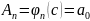Коэффициенты в формуле Тейлора являются значениями частных от деления многочлена на , на , на , это значение частного при делении на , на .

Пример: .

	1	-1	0	2	-1	3
2	1	1	2	6	11	25
2	1	3	8	22	55
2	1	5	18	58
2	1	7	32
2	1	9
2	1

.

Разложить дробь на простейшие.

.

Многочлены над полем комплексных чисел

К. Гаусс (1777-1855) в нач. XIX в. доказал Основную теорему алгебры.

Всякий многочлен над полем комплексных чисел имеет хотя бы один корень, принадлежащий этому полю.

Следствие: Всякий многочлен над полем комплексных чисел имеет ровно n корней, считая их кратность.

Доказательство:

По основной теореме о существовании корня этот многочлен имеет хотя бы 1 корень.

.

Тогда по критерию корня

, степени .

По основной теореме

, .

Если , то корень , .

.

На n- ом шаге - многочлен нулевой степени.

.

.

.

Где - корни.

, где .

.

2. Всякий многочлен ст. является приводимым над полем P.

- приводим.

Неприводимыми многочленами над полем комплексных чисел являются многочлены 1-ой степени.

Многочлены над полем действительных чисел

с действительными коэффициентами

, (1)

.

По основной теореме алгебры этот многочлен имеет хотя бы один комплексный корень (R C). Этот корень может быть действительным.

Теорема о сопряженности комплексных корней многочлена с действительными коэффициентами:

Если является корнем многочлена (1) с действительными коэффициентами, то число, сопряженное к является корнем .

Доказательство:

Так как – корень, то , . (2)

Из теории комплексных чисел

,

,

,

,

.

,

. (3)

, т.е. является корнем многочлена. Ч.т.д.

Покажем, что кратность корней и будет одинаковой.

Пусть - корень многочлена k-ой кратности, - корень многочлена -ой кратности.

.

Учитывая определение кратности

;

, .

Надо доказать, что .

1. Пусть , тогда ;

.

,

.

Получили многочлен второй степени с действительными коэффициентами .

– многочлен с действительными коэффициентами, любая его степень будет многочленом с действительными коэффициентами.

.к. с действительными коэффициентами, ψ тоже с действительными коэффициентами.

Тогда частное = с действительными коэффициентами.

, => является корнем этого многочлена.

.

.к. – корень, то тоже корень (по предыдущей теореме).

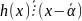, но , т.к. и => получили противоречие.

Предположение, что не верно.

2. , то аналогично получили бы противоречие.

=> => кратности корней многочлена с действительными коэффициентами одинакова.

При этом говорят, комплексные корни многочлена с действительными коэффициентами попарно сопряжены.