Взаимно-простые многочлены и их свойства.

Определение. 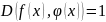, тогда – взаимно-простые.

Теорема 1 (критерий):

, взаимно-простые  над P .

Доказательство:

1. Необходимость этого условия вытекает из теоремы о линейном представлении НОД.

2. Достаточность.

Дано:

Доказать:

Метод «от противного».

Пусть

1

Теорема 2:

и , то .

Доказательство:

Т.к. по теореме 1

|

,

.

Теорема 3:

, то

Доказательство:

Из что над P

Если бы , то

общий делитель ,

а по условию - противоречие =>

.

Теорема 4:

Если и и , то

Доказательство:

,

.

Наименьшее общее кратное двух и нескольких многочленов.

Многочлен называется общим кратным многочленов , если ,

КОН двух или нескольких многочленов называется такой многочлен m(x) над P, который является общим кратным: 1) ; 2) 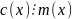; - общее кратное.

Теорема:

Для любых двух отличных от нуля многочленов существует НОК.

Теорема:

Если , , то является НОК этих многочленов, .

Доказательство:

Т.к.

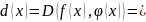
- общее кратное.

общее кратное

По теореме 2:

k, q – взаимно простые.

.

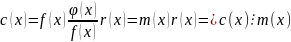Теорема:

Если – многочлены над полем P и , , …, , 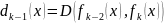то .

Теорема:

Если – многочлены над полем P и , , , …, , то .

Значение многочлена от числа. Корни многочлена. Деление многочлена на линейный двучлен.

Схема Горнера.

над P.

Пусть c – любое число из P.

– число из P.

Это число называется значением многочлена при .

Пример:

Определение. Число c называется корнем многочлена , если

1 – корень многочлена .

, ,

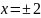, 2i, -2i,

, I, -i.

Замечание: Если , то .

Деление многочлена на линейный двучлен

ax+b, a≠0

По теореме о делении с остатком:

для над P найдется ,

ст.

ст.

ст. или

– число из P.

В правой части этого равенства раскроем скобки и сгруппируем по степеням x.

Из равенства многочленов получим равенство их коэффициентов.

				…
c				…		r=

Пример:

	1	0	2	0	0	0	3	-7
2	1	2	6	12	24	48	99	191

Теорема Безу. Следствие из теоремы Безу.

Теорема:

Остаток от деления многочлена на линейный двучлен равен значению многочлена при .

Доказательство:

т. к. делиться на , то остаток от деления является числом 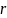не зависящим от x

Следствие (критерий того, чтобы многочлен имел корень):

Число является корнем многочлена .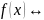

Доказательство:

1. Необходимость:

Дано: c – корень .

Доказать: .

(т.к. c – корень).

По теореме Безу .

2. Достаточность:

Дано: .

Доказать: c – корень .

(т.к. ).

.

Замечание:

По схеме Горнера можно решать следующие задачи:

1. Найти частное и остаток от деления многочлена на линейный двучлен.

2. Находить значение многочлена при любом .

3. Определять является ли число c корнем многочлена.

Нахождение коней многочлена равносильно нахождению его линейных делителей вида .