Теорема Вейерштраса. Теорема Ферма и ее приложение. Правило множителей Лагранжа. Примеры
Пусть
- функции n переменных x
= (
).
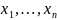Рассмотрим задачу с ограничениями типа
равенств и неравенств:
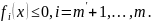
Также рассмотрим примеры:
=
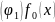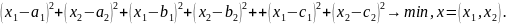
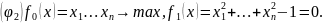
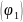формализует такую задачу: найти на
плоскости точку, сумма квадратов
расстояний от которой до трех данных
точек была бы минимальной.
Конечно,
не каждая задача типа
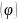имеет решение. Однако, как и для функций
одного переменного, можно сформулировать
теорему, которая во многих случаях
гарантирует существование решения.
Обозначим совокупность допустимых точек в задаче через С. Иначе говоря, С состоит из трех точек х, для которых
Множество
С называется ограниченным, если существует
константа A > 0 такая, что
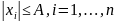для любой точки x = (
)
из С. Например, множество
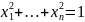ограничено, в частности ограничена
окружность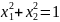
,
а множество
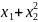(парабола)
не является ограниченным множеством.
Теорема
Вейерштрасса. Пусть в задаче
функции
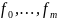непрерывны, а совокупность С допустимых
точек в
ограничена. Тогда решение обеих задач:
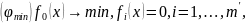
и
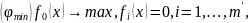
существует.
Следствие.
Пусть функция
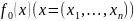непрерывна для любого x.
Тогда если
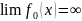при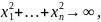 
то
решение задачи без ограничений
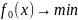существует.
Теперь
сформулируем две теоремы, которые
позволят нам описать правило решения
задач типа(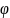
).
Теорема
Ферма. Пусть в точке
существуют все частные производные
функции
.
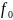Если точка
доставляет локальный экстремум (минимум
или максимум) этой функции, то
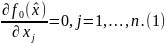
Точки, для которых все частные производные равны нулю, называются стационарными. Соотношения (1) являются, разумеется, необходимыми условиями.
Приведем
пример приложения этой теоремы. Решим
задачу
.
Решение задачи существует в силу
следствия теоремы Вейерштраса. Обозначим
его
.
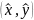Имеем
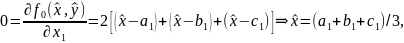
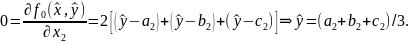
Ответ.
есть центр масс треугольника (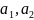
),
(
),(
).
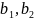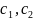Теперь
рассмотрим общую задачу
,
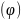в которой, правда, неравенства отсутствуют.
Составим такую сумму:
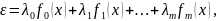где
.
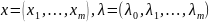Эту функцию
называют функцией Лагранжа. Числа
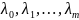называются множителями Лагранжа.
Общий принцип Лагранжа, описание которого вынесено нами в эпиграф, можно коротко выразить так: для решения задачи ( ) надо составить функцию Лагранжа, а затем поступить с ней так, как если бы переменные ( ) были независимы (т. е. применить теорему Ферма). Полученные уравнения, а именно уравнения:
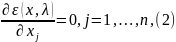
дополненные уравнениями связи
надо решить
относительно
,
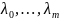и среди этих решений выбрать нужное.
Это правило основывается на следующей теореме.
Теорема (правило множителей Лагранжа).
Пусть функции
определены в некотором параллелепипеде
П(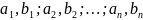
),
содержащим внутри себя точку
.
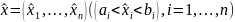Пусть далее все функции
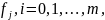и все частные производные
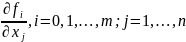непрерывны
в этом параллелепипеде. Тогда если
допустимая точка
доставляет локальный экстремум (максимум
или минимум) в задаче (
),
то найдутся числа
,
не равные одновременно нулю и такие,
что
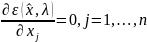
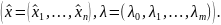
В (2) и (3) имеется n+m уравнений с n+m+1 неизвестным. Но надо иметь в виду, что множители Лагранжа можно умножать на любую константу, отличную от нуля.
Надо иметь в виду, что множители Лагранжа можно умножать на любую константу, отличную от нуля. Таким образом, всегда можно домножить так, чтобы один из множителей Лагранжа равнялся единице. Тогда в (2) – (3) число уравнений фактически равно числу неизвестных.
Далее.
Уравнения (2) наиболее содержательны,
если
.
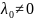Ведь если
,
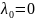то уравнения (2) отражают лишь вырожденность
ограничений и не связаны с функцией,
экстремум которой ищется. Но вообще-то
заранее считать, что
отлично от нуля, нельзя. Приведем пример,
показывающий, что правило множителей
Лагранжа при дополнительном допущении
может стать неверным.
Пример.
Рассмотрим задачу (рис. 6.1):
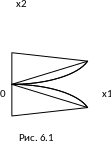
Из рисунка
видно, что единственным решением задачи
является точка
.
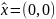Попробуем теперь составить функцию
Лагранжа с
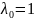и применить алгоритм Лагранжа:
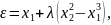откуда
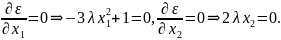
Уравнение
связи имеет вид
.
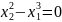Написанные уравнения, как легко видеть,
несовместны.
Правило множителей Лагранжа позволяет дать следующий рецепт поиска решений задачи ( ) с равенствами. Разобьем его на те же 4 этапа.
1 этап – формализация задачи. Требуется привести задачу к виду ( ) с m’= m.
2 этап – применение принципа Лагранжа, т. е. составление системы уравнений
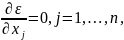
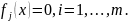
3 этап состоит в нахождении всех стационарных точек. При этом бывает полезно сначала выяснить вопрос о том, может ли равняться нулю или нет.
4 этап состоит в переборе всех стационарных точек и выборе тех, где функция имеет минимальное (максимальное) значение.
Метод множителей Лагранжа применяется:
при решении задач нелинейного программирования, возникающих во многих областях (например, в экономике);
основной метод решения задачи об оптимизации качества кодирования аудио и видео данных при заданном среднем битрейте (оптимизация искажений).