4. Максимумы и минимумы в алгебре и анализе

Алгебра щедра. Зачастую она дает больше, чем у нее спрашивают.

Даламбер

Неравенство между средним геометрическим и средним арифметическим (общий случай).

Докажем следующую теорему. Для любых неотрицательных чисел x₁,…,x_n имеет место неравенство

Левая часть неравенства (1) называется средним геометрическим чисел , правая называется их средним арифметическим. Таким образом, не только для n = 2, но и при любом n среднее геометрическое не превосходит среднего арифметического. Неравенство (1) является точным. Если все числа равны, оно обращается в равенство.

Существует большое число доказательств неравенства (1). Одно из них дано французским математиком О. Коши.

Сначала покажем, как по методу Коши доказать неравенство (1) для n = 3. Для этого выведем (1) при n = 4, а затем перейдем к n = 3. Для n = 4 неравенство (1) сразу следует из двукратного применения неравенства (1) (для n = 2):

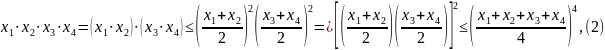
т.е. неравенство (1) для n = 4 доказано.

А теперь получаем (применив (2))

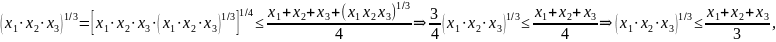
Что доказывает (1) для n = 3.

Теперь докажем (1) в общем случае. Во-первых, отметим, что точно так же, как выше было доказано неравенство (1) для n = 4, можно доказать его для n = 8, затем для n = 16 и т. д. – для любого n = 2^k, k = 2, 3, . . .

Применим «метод перехода», который был уже использован нами при переходе от четырех к трем. Пусть неравенство для n = m + 1 уже доказано. Докажем его для n = m. Имеем по нашему допущению

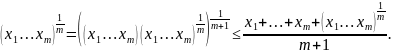
Отсюда

Неравенство (1) доказано полностью.

Итак, решение данной задачи можно проводить следующим образом (пошагово):

Рассмотрим вспомогательную экстремальную задачу:

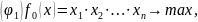
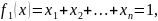
Функции непрерывны и их частные производные непрерывны. Совокупность допустимых точек ограничена, ибо 0 ≤ x_k ≤ 1 для любого k. Значит, по теореме Вейерштрасса решение существует. При этом, конечно, 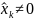, ибо иначе 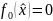, в то время как существуют допустимые элементы, для которых .

Решение будет, конечно, и локальным минимумом в задаче ( ), откуда оно будет локальным минимумом и в задаче без неравенств.

1. Формализация:

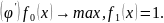
Функция Лагранжа для

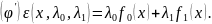
2. Необходимое условие – правило множителей Лагранжа:

3. Нахождение стационарных точек. Обозначим произведение через А. Тогда

Если допустить, что , то сразу приходим в противоречие с тем, что оба множителя, 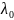и , не могут быть нулями. Тогда получаем , т.е. .

4. Вследствие того, что стационарная точка в ( ) единственна, она и доставляет решение задачи.

Теперь докажем нужное неравенство. Пусть – любые неотрицательные числа. и Тогда и значит, по доказанному

что и требовалось доказать.

Неравенство между средним арифметическим и средним квадратическим.

Пусть x₁,…,x_n – некоторые числа. Их средним квадратическим называется число . Имеет место следующая теорема:

Для любых чисел x₁,…,x_n выполняется неравенство

т. е. среднее арифметическое всегда не превосходит среднего квадратического. Неравенство (1) является точным. Если все числа равны, оно обращается в равенство.

Неравенство (1) можно также доказывать по-разному. Но самое простое, пожалуй, такое доказательство. Имеем:

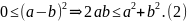
Возводя среднее арифметическое в квадрат и воспользовавшись далее неравенством (2), получим:

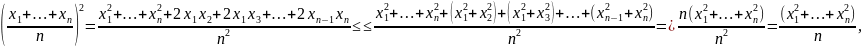
что и требовалось.

Сопоставляя неравенство между средним геометрическим и средним арифметичким и доказанное неравенство (1), получаем, что для любых неотрицательных чисел 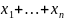имеет место точное неравенство:

В частности, при n = 2 получаем 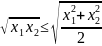. Этому неравенству можно без труда придать геометрическое содержание. Из него, например, сразу следует, что среди прямоугольников, вписанных в круг, наибольшую площадь имеет квадрат. Эта задача в свою очередь допускает по меньшей мере два стереометрических обобщения. Одно из них такое: среди прямоугольных параллелепипедов, вписанных в шар, найти параллелепипед наибольшего объема. Другое обобщение: среди цилиндров, вписанных в шар, найти цилиндр наибольшего объема. Обе эти стереометрические задачи исследовал Кеплер.