2. Экстремум функции нескольких переменных

Как и в случае одной переменной, функция z = f(x,y) имеет узловые, определяющие структуру графика точки. В первую очередь это точки экстремума.

Определение.

Точка называется точкой максимума (минимума) функции z=f(x, y), если существует окрестность точки М, такая, что для всех точек (х, у) из этой окрестности выполняется неравенство

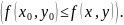
На рис. 2.1 точка А(х₁, у₁) – есть точка минимума, а точка В(х₂, у₂) – точка максимума.

Стоит обратить внимание на то, что экстремум (максимума и минимума) функции носит локальный характер, так как речь идет о максимальном и минимальном значении лишь в достаточно малой окрестности точки (х₀, у₀).

Сформулируем необходимое условие экстремума – многомерный аналог теоремы Ферма.

Теорема.

Пусть точка (х₀, у₀) – если точка экстремума дифференцируемой функции z = f(x, y). Тогда частные производные в этой точке равны нулю.

□ Пусть точка М( ) – точка максимума. Зафиксируем одну из переменных, например у, полагая у = у₀. Тогда получим функцию одной переменной , которая, очевидно, будет иметь максимум при х = х₀. Согласно теореме Ферма . Аналогично можно доказать, что и

Точки, в которых выполнены необходимые условия экстремума функции z = f(x, y), т.е. частные производные 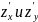равны нулю, называются критическими или стационарными.

Необходимое условие экстремума можно переформулировать также следующим образом: в точке минимума или максимума дифференцируемой функции градиент равен нулю. Можно доказать и более общее утверждение – в точке экстремума обращаются в нуль производные функции по всем направлениям.

Равенство частных производных нулю выражает лишь необходимое, но не недостаточное условие экстремума функции нескольких переменных.

На рис. 2.2 изображена так называемая седловая точка М( ). Частные производные равны нулю, но, очевидно, никакого экстремума в точке М( ) нет.

Такие седловые точки являются двумерными аналогами точек перегиба функций одной переменной. Задача заключается в том, чтобы отделить их от точек экстремума. Иными словами, требуется знать достаточное условие экстремума.

Теорема (достаточное условие экстремума функции двух переменных).

Пусть функция z=f(x, y):

а) определена в некоторой окрестности критической точки , в которой

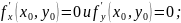
б) имеет в этой точке непрерывные частные производные второго порядка Тогда, если

∆ = АС – В² > 0, то в точке (x₀, y₀) функция z = f(x, y) имеет экстремум, причем если А < 0 – максимум, если A > 0 – минимум. В случае ∆ = АС – В² < 0, функция z = f(x, y) экстремума не имеет. Если ∆ = АС – В² = 0, то вопрос о наличии экстремума остается открытым.

Исследование функции двух переменных на экстремум рекомендуется проводить по следующей схеме:

1. Найти частные производные функции

2. Решить систему уравнений и найти критические точки функции.

3. Найти частные производные второго порядка, вычислить их значения в каждой критической точке и с помощью достаточного условия сделать вывод о наличии экстремумов.

4. Найти экстремумы (экстремальные значения) функции.

Пример:

Найти экстремумы функции

Решение.

1. Находим частные производные

2. Критические точки функции находим из системы уравнений:

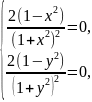
Имеющей четыре решения (1; 1), (1; -1), (-1; 1) и (-1; -1).

3. Находим частные производные второго порядка , вычисляем их значения в каждой критической точке и проверяем в ней выполнение достаточного условия экстремума.

Например, в точке (1; 1) А = zⁿ(1; 1) = -1; В = 0; С = -1.

Так как ∆ = АС – В² = (-1)² – 0 = 1 > 0 и А = -1 < 0, то точка (1; 1) есть точка максимума.

Аналогично устанавливается, что (-1; -1) – точка минимума, а в точках (1; -1) и (-1; 1), в которых ∆ = АС – В² < 0, - экстремума нет. Эти точки являются седловыми.

4. Находим экстремумы функции z_max = z(1; 1) = 2, z_min = z(-1; -1) = -2.