15. Понятие о погрешностях измерений. Способы выражения погрешности измерений.

Для количественной оценки используется понятие «погрешность измерений» (чем меньше погрешность, тем выше точность). Оценка погрешности измерений – одно из важных мероприятий по обеспечению единства измерений.

По способу выражения - абсолютные, относительные и приведенные

Абсолютная погрешность определяется как разность результата измерения х от истинного или действительного значения:

= -х_ист  = -х_д.

Выражается в единицах измеряемой величины.

Пример. При измерении длины детали l получен ряд значений: l₁ = 10,55 мм; l₂ = 10,57 мм, …, l_п = 10,56 мм; вычислено среднее значение

l_ср = 10,56мм -

Погрешности:

 l₁= l₁ - l_ср=10,55 мм - 10,56 мм = - 0,01 мм;

 l₂= l₂ - l_ср = 10,57мм - 10,56 мм=+ 0,01 мм;

l_п = l_n - l_ср = 10,56 мм - 10,56 мм = 0,00

являются абсолютными погрешностями.

Относительная погрешность - это погрешность измерения, выраженная отношением абсолютной погрешности измерения () к действительному значению измеряемой величины (хд):

 = ± /х_д,  = ± /х_д 100%

Пример. Имеем действительное значение длины детали l= 10,00 мм и абсолютную погрешность l =0,01 мм. Относительная погрешность

= l/ l = 0,001 = 1 • 10 ^-3

= l/ l = 0,001 • 100 = 0,1 %.

Приведенная - это погрешность измерения, выраженная отношением абсолютной погрешности измерения () к нормированному значению измеряемой величины (х_н):

 = ± /х_н

Например, х_н = х_мах , где х_мах - максимальное значение измеряемой величины.

17. Взаимосвязь между погрешностью и числом измерений.

Среднее арифметическое из ряда измерений всегда имеет меньшую погрешность, чем погрешность каждого определенного измерения. Это отражает и формула (4.4), определяющая фундаментальный закон теории погрешностей. Из него следует, что если необходимо повысить точность результата (при исключенной систематической погрешности) в 2 раза, то число измерений нужно увеличить в 4 раза; если требуется увеличить точность в 3 раза, то число измерений увеличивают в 9 раз и т. д.

18. Погрешности, подчиняющиеся нормальному закону распределения. Использование дифференциальной и интегральной функции вероятности в определении погрешности измерений.

Наиболее универсальным способом описания случайных величин яв-ся отыскание их интегральных или дифференциальных функций распределения

Интегральная ф-я распределения вероятности F(x) определяет вероят-ть того, что отдельный результат будет меньше аргумента.

Чем больше х, тем больше вероятность того, что ни один результат измерений не превысит этого значения, то есть F(x) – неубывающая функция:

F(x2)>F(x1), если х2>х1.

При изменении х от -∞ до +∞ ф-я F(x) меняется от 0 до1.

Вер-ть того, что результат сравнения окажется в интервале [x1;x2], равна разности значений F(x) на границах этого интервала: P(x1≤x≤x2)=F(x2)-F(x1)

Функция плотности распределения вероятности р(х) связана с ф-ей распределения вер-ти F(x) соотношением

Р(х)=F’(x)

Поэтому р(х) часто называют дифференциальной функцией распределения вероятности.

При расширении интервала до бесконечности рассматриваемое событие становится достоверным. Поэтому площадь, ограниченная графиком ф-и р(х) и осью абсцисс, равна 1.

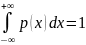
Если справедливо соотношение р(х)=F’(x), то функция может быть получена интегрированием р(х) в соответ-щих пределах:

Так как F(x) – неубывающая функция, то ее производная не может быть отрицательной, то вероятность всегда р(х)>0.

Вероятность того, что отдельный результат окажется в интервале [x1;x2], равна площади, ограниченной графиком функции р(х), осью абсцисс и перпендикулярами к ней на границах интервала, то есть соответствуют уравнению

Описание отсчета или результата измерения с помощью законов распределения вероятности яв-ся наиболее полным, но не всегда удобным. Во многих случаях ограничиваются приближенным описанием закона распределения вероятности с помощью его числовых характеристик, или моментов. Все они представляют собой некоторые средние значения, причем, если усредняются величины, отсчитываемые от начала координат, моменты называют начальными, а если от центра закона распределения – центральными. Первый начальный момент – среднее значение

Сред. значение характеризует математическое ожидание отсчета при бесконечном повторении процедуры измерения.

Второй центральный момент – дисперсия .

Подчиняется ли распределение нормальному з-ну можно узнать из гистограммы, если при ее построении соблюд след условия: 1) интервалы ΔQ по возможности должны быть одинаковыми, 2) количество интервалов завис от кол-ва измерений, 3) масштаб выбирается так, чтобы высота гистограммы относ к основанию примерно 5:8.

Существует неск критериев согласия, по кот проверяется соотв распределению. Один из них – критерий Пирсона

Вероятность того, что случайное число примет значение, меньшее аргумента этой функции определяется по интегральной функции χ²-распределения.