Лабораторная работа № 3 Исследование систем подчинённого регулирования с последовательно-параллельной коррекцией

1. Цель работы:

1. Изучить методику расчёта систем подчинённого регулирования с последовательно-параллельной коррекцией.

2. Определить переходные характеристики систем подчинённого регулирования с последовательно-параллельной коррекцией и сравнить их с соответствующими характеристиками систем при последовательной коррекции.

3. Оценить влияние изменения параметров систем регулирования на изменения переходных характеристик при последовательной и последовательно-параллельной коррекциях.

2. Постановка задачи

Упрощённая структурная схема системы с последовательно-параллельной коррекцией представлена на рис.1

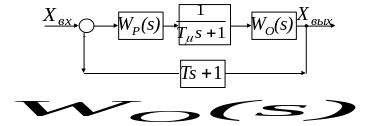
В этой системе регулятор компенсирует большую постоянную времени объекта и корректирует коэффициент усиления системы, определяемый постоянной интегрирования

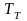
. (1)

В системах с последовательной коррекцией выполняется соотношение

где - коэффициент пропорциональности (коэффициент настройки).

При постройке на технический оптимум часто принимают, что . Конечно коэффициент настройки можно уменьшить, что приведет к увеличению коэффициента усиления системы, но тогда автоматически возрастёт и перерегулирование.

Рассмотрим влияние дифференцирующего звена на характеристики системы с последовательно-параллельной коррекцией

. (2)

Запишем характеристическое уравнение замкнутой системы через собственную частоту колебаний и коэффициент демпфирования:

;             . (3)

Известно, что при настройке системы подчинённого регулирования на технический оптимум, коэффициент демпфирования равен

. (4)

Из (4) видно, что равенство может выполняться при и тогда , что свидетельствует о отсутствии параллельной коррекции и настройке системы подчинённого регулирования на технический оптимум при . Если же то система настраивается на технический оптимум с использованием параллельной коррекции при коэффициенте настройки меньшем, чем 2. Такая настройка применяется тогда, когда требуется повысить быстродействие системы, что часто имеет место при больших значениях ( ). Отношение ( ), будучи поставленное в соотношение (4), позволяет вычислить отношения , которые определяет коэффициент демпфирования. При отношение =2, что указывает на отсутствие параллельного корректирующего устройства, а при равенство (4) выполняется при коэффициенте демпфирования больше оптимального ( ).

Вторым важным свойством последовательно-параллельной коррекции является малая чувствительность системы регулирования к изменениям параметров, например коэффициента усиления. Если принять, что и по выражению (4) построить график , то получим, что изменение от 0,4 до 2,8 мало влияет на изменения коэффициента демпфирования.

Проиллюстрируем теоретические положения примерным расчётом (рис.2). На рис.2.А представлена структурная схема системы с последовательной коррекцией. Параметры регулятора определены по известному соотношению с коэффициентом настройки равным 2:

. (5)

Из (5) получаем передаточную функцию регулятора

.

Принимаем ; .

Рис.2. Структурные схемы систем с последовательной (рис.2.А) и последовательно-параллельной коррекцией (рис.2.B,C)

Передаточная функция реального дифференцирующего звена имеет вид:

.

Используя выражение (4) для принятого отношения определяем коэффициент настройки ;

(6)

Для новых коэффициентов настройки и определяем новые параметры регуляторов, для которых на рис.2.Б рис.2.В представлены структурные схемы системы. Уменьшение коэффициентов настройки приводит к увеличению коэффициента усиления разомкнутой системы с последовательно-параллельной коррекцией, соответственно в 1.55 и 28,98 раза, по сравнению с коэффициентом усиления разомкнутой системы с последовательной коррекцией. Это приводит к существенному повышению быстродействия при практически неизменной величине перерегулировании. На рис.3 приведены три кривые с разными коэффициентами

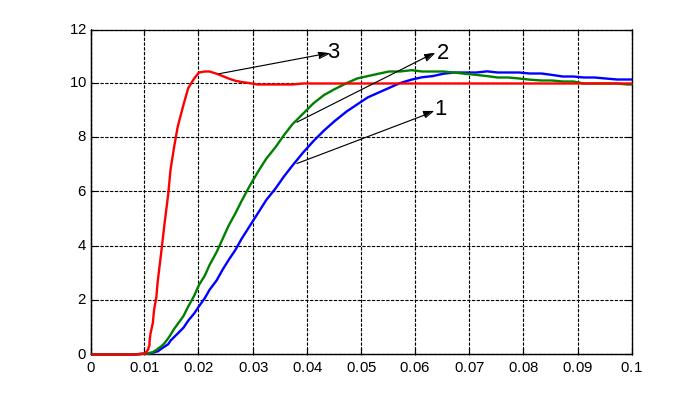
Рис.3. Результат моделирования структурных схем, представленных на рис.2

(1 - коэффициент настройки равен 2; 2 - коэффициент настройки равен 1,29; 3 - коэффициент настройки равен 0,069)

настройки: коэффициент 2 соответствует системе с последовательной коррекцией, коэффициенты 1,29 и 0,069 - системам с последовательно – параллельной коррекцией.

Рассмотрим процедуру исключения дифференцирующей цепочки. Учитывая, что регулятор компенсирует “большие” постоянные времени объекта, структурная схема системы, настроенной на технический оптимум, упрощается (рис.4).

Операцию дифференцирования можно исключить, осуществив структурные преобразования (рис.5).

Рис.5. Преобразованная структурная схема внутреннего контура.

Определим передаточную функцию замкнутой системы, соответствующий преобразованной структуре (рис.5). Передаточная функция замкнутого внутреннего контура имеет вид:

.

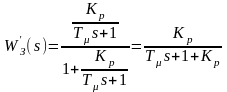Окончательно получаем

. (7)

Если положить что

;           , (8)

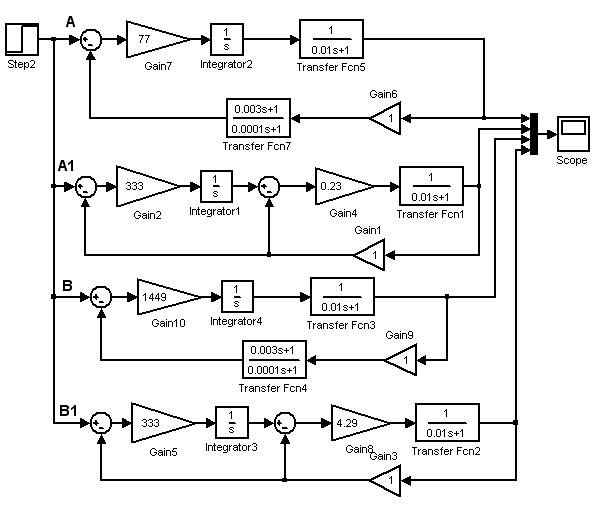
Рис.6. Схемы исходной (последовательно-параллельная коррекция) и преобразованной структурных схем, представленных в пакете MatLab

то структурные схемы, представленные на рис.4 и рис.5, будут одинаковы, так как характеризуются идентичными передаточными функциями.

Проведём соответствующие расчёты. В предыдущем примере было получено

, , , .

Согласно (8) имеем

; ; .

;

.

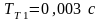На рис.6 представлены четыре структурные схемы. Схемы (рис.6.А и рис.6.В) соответствуют исходной схеме, в который в обратной связи стоит последовательно-параллельное корректирующее устройство. Схемы (рис.6.А1 и рис.6.В1) соответствуют преобразованным структурам с разными значениями .

Переходные характеристики (рис.7) показывают, что выходные координаты схемы рис.6.А совпадают с выходными координатами рис.6.А1, а выходные координаты схемы рис.6.В совпадают с соответствующими координатами рис.6.В1. В то же время схемы, представленные на рис.6.В, характеризуются большим быстродействием при одинаковом перерегулировании.

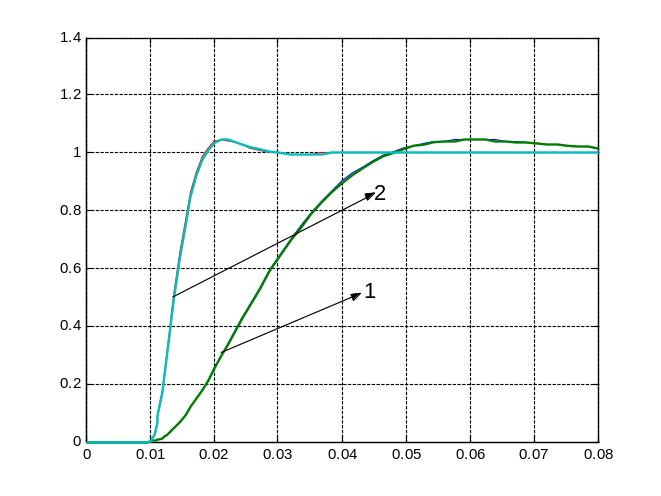
Рис.7. Переходные характеристики, соответствующие структурным схемам рис.6

(1 - рис.6.А и рис.6.А1, 2 - рис.6.В и рис.6.В1)

Преобразование структурной схемы и изменение ее параметров приводит к увеличению быстродействия. В частотной области преобразованной системе соответствуют преобразованные частотные характеристики: увеличена частота среза при сохранении запаса по фазе, что иллюстрируется расчетами (Программа №1)

%Пограмма №1