Методы решения слау

Методы решения СЛАУ подразделяются на точные и итерационные.

Точные методы

Точные – это методы, которые определяют решение при помощи конечного числа арифметических операций.

При этом, если исходные данные и вычисления точны, то получается точное решение (методы Крамера, Гаусса).

Точные методы выполняются в два этапа:

• преобразование исходной СЛАУ к более простому виду;

• решение упрощенной системы и получение неизвестных.

Приближенные (итерационные) методы

Предварительно задаются некоторыми приближенными значениями неизвестных , ..., . Из этих значений тем или иным способом получают новые ‘’улучшенные’’ приближенные значения , ..., . С новыми значениями поступают также.

При выполнении определенных условий после бесконечного числа шагов можно получить точное решение.

На практике вычисления прерывают при достижении заданной точности ε. Для этого на каждой итерации с заданной точностью сравнивают два последовательных приближения

Если выполняются условия

, , ... , ,

то полученные на i - итерации значения , ..., считаются решением СЛАУ.

Метод Гаусса (последовательного приближения неизвестных)

_{Представим СЛАУ в скалярной форме (4.2)}

,

где А = ; x = ; b = ;

1. Последовательно исключая неизвестные, приводим матрицу коэффициентов А к треугольному виду,

2. Находим неизвестные, начиная с x_n, x_n-1, x_n-2, ... , x₂, x₁.

Итерационные методы решения слау

Итерационные методы особенно эффективны при большом порядке СЛАУ.

Предварительно приведем систему (4.1) к виду

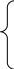, где ,

, (5.1)

........................

,

Исходя из начального приближения , получают векторы ,..., по рекурентной формуле

. (5.2)

Здесь F_k – некоторая функция, зависящая от матрицы коэффициентов А системы (4.2), правой части , номера приближения k и предыдущих приближений .

Метод имеет 1-й порядок, если F_k не зависит от , а зависит только от .

Метод стационарный, если F_k не зависит от k.

Простейший случай: если F_k - линейная функция, то общий линейный метод 1 – го порядка должен иметь вид

(5.3)

Здесь А – квадратная матрица, - вектор.

Метод Якоби (простой итерации)

К виду (5.3) можно привести, например, выделением диагональных элементов (для i – строки)

, ^{i = 1, 2, ..., n (5.4)}

Строим последовательность векторов, начиная с произвольного вектора ( , i = 1, 2, ..., n)

, , ... , ,

где , i = 1, 2, ..., n (5.5)