Составление тестируемой кодовой комбинации crc – кода (7, 4)
Для решения задачи построения декодера необходимо составить разрешенную кодовую комбинацию CRC–кода (7,4), соответствующую безызбыточной комбинации 1100010.
По исходным данным имеем образующий полином двоичного эквивалента 1011:
x3+x1 + 1.
В соответствии с методом кодирования, рассмотренным в [4], получаем:
x
6+x5+
x x3 +x+1
x
6+x4+x3
x3+x2
+ x
x5+x4+x3+x
x5+x3+x2
x4+x2+x
x4+x2+x
0
В дальнейшем проектировании будем использовать полученную комбинацию для проверки правильной работы проектируемых устройств и проекта в целом.
Построение декодирующего устройства циклического кода для обнаружения однократных ошибок
Процедура обнаружения ошибки сводится
к делению принятой комбинации на
образующий полином
и анализу остатку от деления
[4]:
если =0, то ошибок нет (разрешенные кодовые комбинации делятся на образующий полином без остатка) или произошел прием с необнаруживаемой ошибкой (под действием искажений одна разрешенная комбинация перешла в другую разрешенную комбинацию).
если ≠0, то произошел прием с ошибкой (обнаруживаемой).
Декодирующее устройство для обнаружения ошибок представляет собой схему деления двоичных полиномов. Такой схемой является сдвиговый регистр, охваченный обратными связями через сумматоры по модулю два (рис. 2).
Рис. 2. Обобщенная схема CRC-декодера
Схема строится по виду образующего
полинома
.
В схеме, построенной по конкретному
образующему полиному, обратной связи
и сумматоры отсутствуют там, где
коэффициенты образующего полинома
.
Перейдем непосредственно к реализации поставленной выше задачи. Построим декодирующее устройство для кода (7, 4) и образующего полинома вида
.
Коэффициенты этого полинома g0=g1=g3=1, g2=0. Число триггеров, равно степени полинома m=3. Получим схему, представленную на рис. 3.
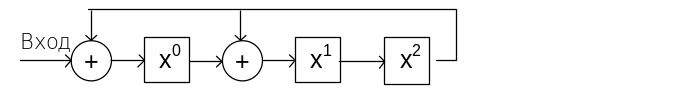
Рис. 3. Схема CRC-декодера с образующим полиномом 1011
В исходном состоянии триггеры сдвигового
регистра обнулены. Принимаемая 7-разрядная
кодовая комбинация символ за символом
вводится в регистр. В течение первых 3
тактов обратная связь не действует,
т.к. триггер
-
в нулевом состоянии. В течение последующих
4 тактов происходит деление: делимое
суммируется по модулю два с делителем,
поступающим через обратные связи. С
поступлением последнего символа деление
завершается. В регистре записан остаток,
по виду которого принимается решение
о наличии ошибок.
Работа декодера на основе образующего полинома x3+x2+x+1 на первых трех тактах описывается следующими уравнениями:
T0(i)=T2(i-l)+C(i),
T1(i)=T0(i-l)+T2(i-l),
T2(i)=T1(i-l),
где
Tj[i] - состояние j- ого триггера на i-ом такте;
Сi - i-ый информационный символ.
1. Работу декодера проиллюстрируем на примере кодирования безызбыточной комбинации, причем не имеющей ошибок, вида
C1C2C3C4C5C6C7 = 1100010.
Такт, i |
Вход, Ci |
Состояния триггеров |
||
Т0[i] |
Т1[i] |
Т2[i] |
||
0 |
- |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
2 |
1 |
1 |
1 |
0 |
3 |
0 |
0 |
1 |
1 |
4 |
0 |
1 |
1 |
1 |
5 |
0 |
1 |
0 |
1 |
6 |
1 |
0 |
0 |
0 |
7 |
0 |
0 |
0 |
0 |
Таблица 1 состояний CRC-декодера
После завершения приема кодовой комбинации все триггеры находятся в нулевом состоянии. Следовательно, остаток R(x)=0 и ошибок нет.
2. Рассмотрим случай однократной ошибки. Пусть под действием помехи искажен 5-ий информационный символ С5, т.е. вместо переданной комбинации 1100010 принята кодовая комбинация 1100110
Такт, i |
Вход, Ci |
Состояния триггеров |
||
Т0[i] |
Т1[i] |
Т2[i] |
||
0 |
- |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
2 |
1 |
1 |
1 |
0 |
3 |
0 |
0 |
1 |
1 |
4 |
0 |
1 |
1 |
1 |
5 |
1 |
0 |
0 |
1 |
6 |
1 |
0 |
1 |
0 |
7 |
0 |
0 |
0 |
1 |
Таблица 2 состояний CRC-декодера |
||||
Получили ненулевой остаток от деления, следовательно, исходная комбинация принята с ошибкой.
С учетом приведенного алгоритма декодирования, а также принципа построения CRC-декодера для обнаружения однократных ошибок, было разработано декодирующее устройство, схема которого приведена на рис. 5. В соответствии с заданием декодер должен был быть разработан на основе логических элементов из библиотеки MAX+PLUS II.
Входы модуля:
in – вход данных (ввод кодовой комбинации);
enable – разрешение работы;
clock – тактирующие импульсы.
reset – обнуление декодера
Выходы модуля:
x[2..0] – для вывода остатка от деления на образующий полином.
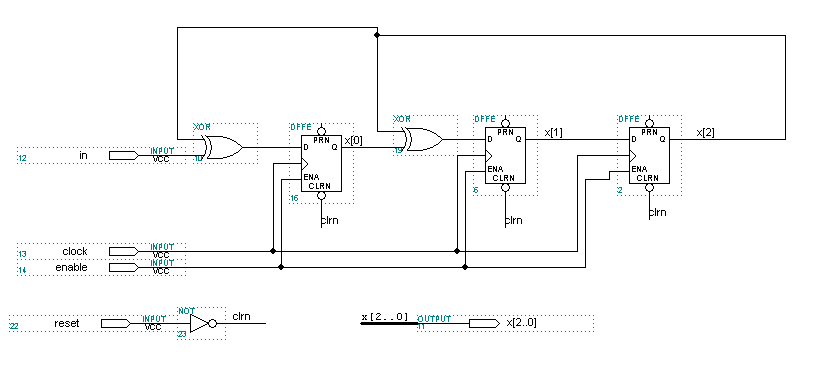
Рис. 4 Схема CRC – декодера на основе логических элементов
Для дальнейшей работы с проектом сохраним устройство в виде графического символа, представленного на рис. 5.
Рис. 5. Символ CRC-декодера
Временные диаграммы, полученные в результате моделирования, приведены на рис. 6 для безошибочного приема комбинации и рис. 7 для приема с ошибкой во 5-м разряде.
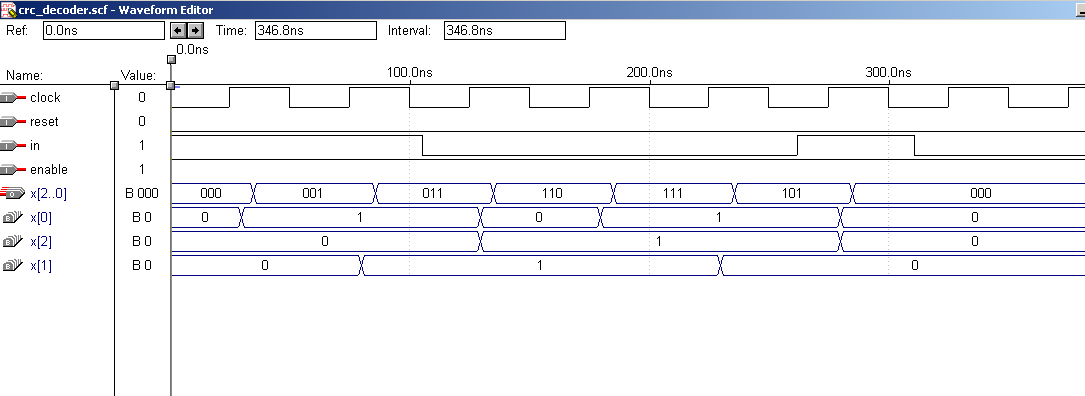
Рис. 6 Временная диаграмма работы CRC-декодера для приема комбинации без ошибки
Рис. 7 Временная диаграмма работы CRC-декодера для приема комбинации с ошибкой в пятом разряде