Неоднозначные нелинейности
Реле с обычным гистерезисом
Математическое описание в форме
Статическая характеристика un = N(xn ,un-1)
Индекс «n» соответствует текущему значению сигнала, индекс «n-1» - предшествующему значению, n=1,2,3…
НЭ9
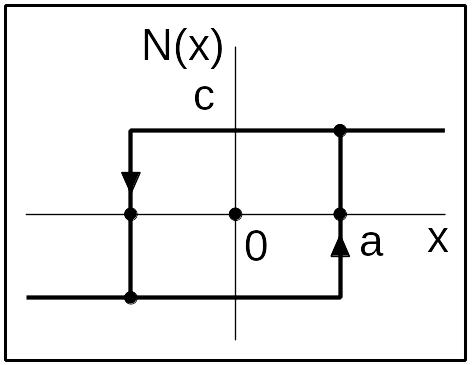
Рис. 9 Н.э. – двухпозиционное реле с гистерезисом (положительным)
|
если | xn |>a то un = sign(xn) если | xn |<a то un = un-1 при значении входного сигнала |x|=а, выходной сигнал скачком изменяет значение с «с» на «-с» |
НЭ10
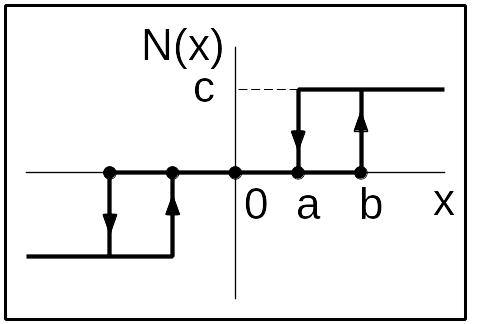
Рис. 10 Н.э. – трёхпозиционное реле с гистерезисом (положительное) |
если |xn |<a то un =0 если a<|xn |<b то un = un-1 если |xn |>b то un = с·sign(xn) при значении входного сигнала |x|=а или |x|=b, выходной сигнал скачком изменяет своё значение, как показано на рисунке10 |
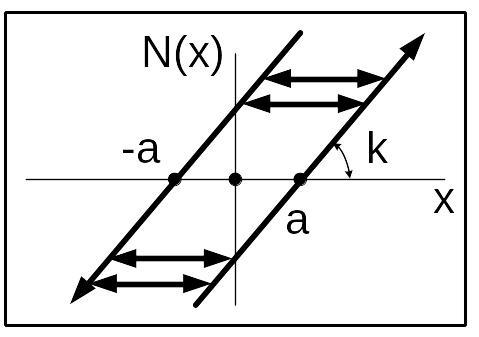
Реле с опережением
Статическая характеристика. Математическое описание в форме
u=N(xn, xn-1, un-1)
НЭ11
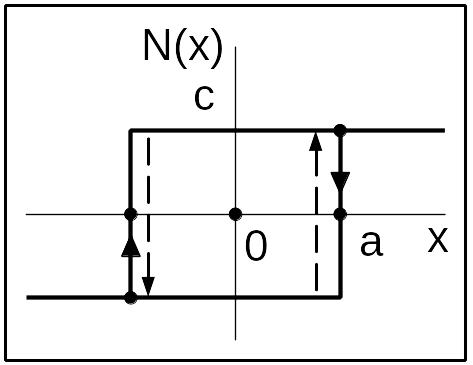
Рис. 11 Н.э. – двухпозиционное реле с отрицательным гистерезисом (с опережением)
|
если | xn|>a то un=c ·sign(xn) если | xn|<a и | xn-1|>a то un=- un-1 если | xn|<a и | xn-1|<a то un= un-1 при значении входного сигнала |x|=а, выходной сигнал скачком изменяет значение, причём изменение может происходить в двух направлениях, как показано на рисунке11. |
НЭ12
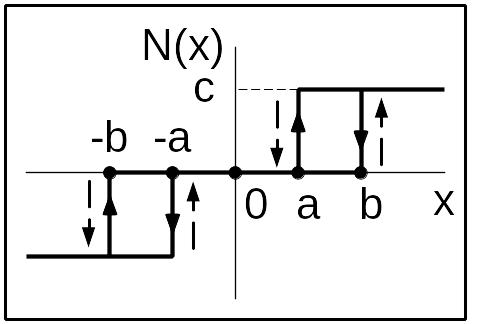
Рис. 12 Н.э. – трёхпозиционное реле с отрицательным гистерезисом (с опережением) |
если |xn |>b то un =c ·sign(xn) если | xn|<a то un=0 если a<| xn|<b и a<| xn-1|<b то un = un-1 если a<| xn|<b и | xn-1|<a то un =c·sign(xn) если a<| xn|<b и | xn-1|<b то un =0
|
Нелинейные характеристики, содержащие люфт.
Статическая характеристика. Математическое описание в форме
u=N(xn, xn-1, un-1)
НЭ13
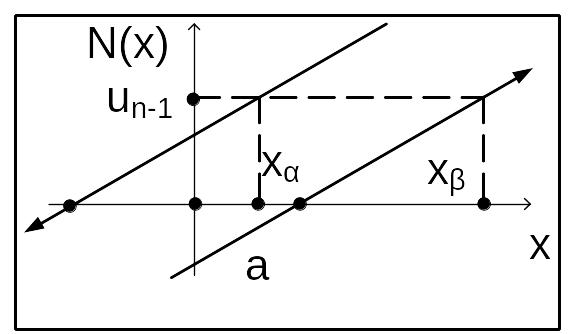
Рис. 13 Н.э. - люфт
|
Вычисляем значения xα и xβ (см. рис. 13а) xα = -a + un-1 /k xβ = a + un-1 /k Если |xα|< |xn|< |xβ| то un= un-1 если |xn|< |xα| то un = k · (xn +a) если |xn|> |xβ| то un = k · (xn +a)
|
Рис. 13а (вспомогательный)
|
|
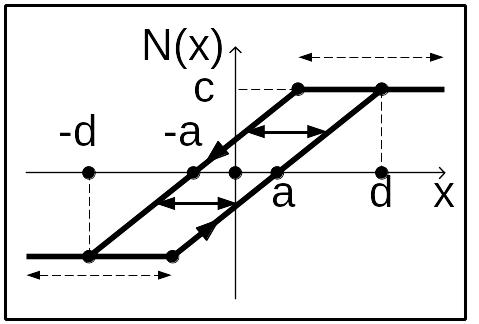
НЭ14
Рис. 14 Н.э. – люфт, ограничение
|
Вычисляем k=c/(d - a) Если |xn|>d то un=c ·sign(xn) если | xn|<d то описание совпадает с нелинейностью люфт |
