§3. Автоколебания в системах управления.

Постановка задачи.

Предположим, что исходная система, содержащая один нелинейный элемент, приведена к виду, показанному на рисунке 1. Входное воздействие будем предполагать импульсным. То есть система выводится из положения равновесия (в некоторую точку фазового пространства), после чего входное воздействие равно нулю.

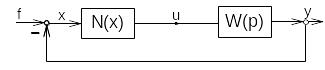
Рис. 1.

Таким образом, мы будем рассматривать собственные движения системы. Нас будет интересовать, имеет ли место в системе автоколебания, и каковы их параметры. С математической точки зрения задача состоит в том, чтобы определить имеются ли предельные циклы Пуанкаре в фазовом пространстве, каковы их параметры. Решить вопрос об устойчивости предельных циклов (после того, как они найдены). Нужно отметить, что поставленная задача значительно труднее, чем задача об исследовании положения равновесия, и её решение в общем виде на сегодняшний день отсутствует.

Академиком А.Андроновым и его учениками (Горьковская школа по теории колебаний) был разработан в середине сороковых годов метод точечных преобразований и с его помощью были найдены точные решения классических задач авторегулирования второго порядка и в некоторых случаях третьего порядка. Отметим, что нелинейные элементы в этих задачах были кусочно-линейными. Дальнейшее продвижение в этом направлении, т.е использование точечного метода для преобразования систем более высокого порядка, связано со значительными трудностями.

Поэтому ниже мы приведем только один результат точного решения задачи изучения автоколебаний для систем сколь угодно высокого порядка, полученный В.А.Якубовичем.

Частотный критерий автоколебательности В.А.Якубовича.

Предварительно нам потребуется формулировка автоколебательной системы. Подчеркнём, что колебания могут быть сколь угодно сложной формы!

Система называется автоколебательной, если удовлетворяются следующие условия:

1.Сигнал на выходе y(t) системы ограничен.

2.При t→∞ имеется бесконечно много перемен знака сигнала y(t).

3.Пусть t_k’ и t_k’’ – бесконечные последовательности моментов времени.

Имеют место соотношения:

(1)

4.Время пребывания сигнала y(t) в промежутках (-∞;α) , (α;β), (β;∞) ограничено величиной Т.

Обратим внимание, что числа α и β являются нижними границами автоколебаний.

Система будет автоколебательной, если ее нелинейный элемент имеет график, показанный на рисунке 2.

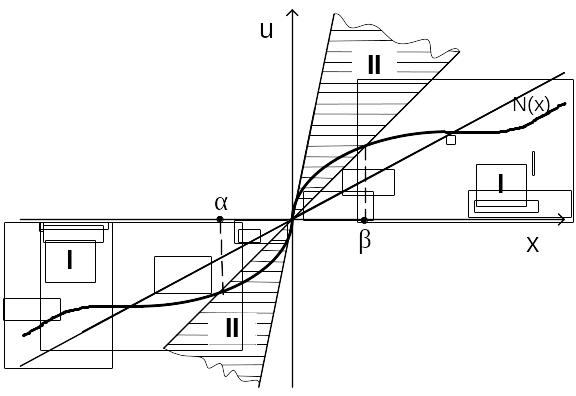
Рис. 2

На рисунке 2 сектор II - это сектор неустойчивости линейной системы сравнения (ЛСС), а сектор I – сектор абсолютной устойчивости исходной системы.

Метод гармонического баланса для исследования автоколебаний, имеющих форму, близкую к синусоиде.

В сороковых годах Л.С.Гольдфарбом был предложен удивительно простой метод [x] определения автоколебаний в системах автоматического управления. Метод не является математически доказанным утверждением и базируется на правдоподобных рассуждениях. Этот метод позднее был с исключительной полнотой развит в работах Е.П.Попова [x]. Сразу же отметим очень важное обстоятельство. Метод не дает информации о жестком или мягком режиме возникновения автоколебаний.

Перейдём к его описанию. Л.С.Гольдфарб обратил внимание, что очень часто автоколебания в технических системах авторегулирования на выходе объекта имеют почти гармонический характер. Запись колебаний выходной координаты y(t) может быть аппроксимировано функцией Asin(Ωt), если соответственно подобрать числа А и Ω. На основе этого наблюдения Л.С.Гольдфарб построил логику своих рассуждений на следующем исходном предположении.

Сигнал на входе нелинейного элемента (x(t)=-y(t)) следует принять равным

x(t)=Asin(Ωt) (2)

где числа А и Ω необходимо вычислить.

Из исходного предположения вытекает, что автоколебания в системе имеют период:

(3)

Сигнал на выходе нелинейного элемента u(t)=N(Asin(Ωt)) является периодической функцией с периодом Т, но форма его колебаний может быть очень далека от гармонической, например, прямоугольная волна и т.д. сигнал u(t) представляет собой ряд Фурье:

(4)

(Для простоты предположим, что постоянная составляющая отсутствует, т.е. D₀=0.)

Далее по логике рассуждений необходимо, чтобы линейный блок пропускал только первую гармонику сигнала u(t), т.е. АЧХ W(p) имело форму фильтра высоких частот.

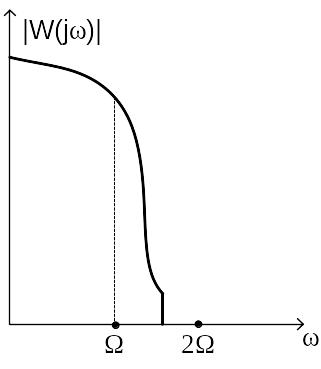
Рис. 3

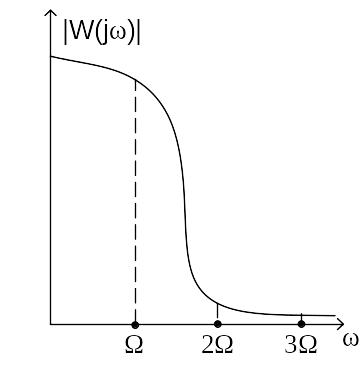
Физически такая АЧХ невозможна у линейного блока, однако допустима ситуация, когда АЧХ имеет форму, показанную на рисунке 4. В этом случае говорят, что линейный блок удовлетворяет «гипотезе фильтра».

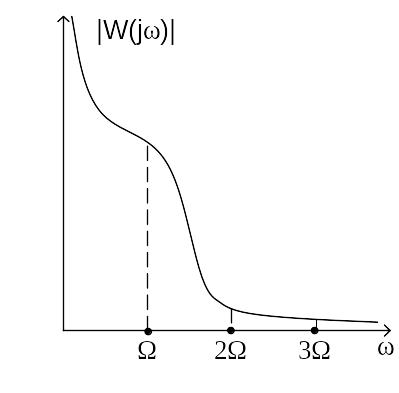
Возможна ситуация, когда АЧХ линейного блока удовлетворяет гипотезе резонанса и имеет вид, показанный на рисунке 5, но этот случай часто встречается в теории колебаний и нехарактерен для задач авторегулирования. Далее будем предполагать, что АЧХ удовлетворяет гипотезе фильтра.

Рис. 4а

Рис. 4b

На рисунке 4а приведена амплитудно-частотная характеристика в случае, когда W(p) не содержит интегрирующее звено, на рисунке 4b – когда содержит.

Рис. 5

Автоколебания – это стационарный процесс, поэтому при его рассмотрении мы предполагаем, что он длится уже достаточно долго, и переходный процесс линейного блока давно затух. Следовательно, на выходе линейного блока мы можем рассматривать только установившийся процесс, который будет равен

(5)

Предполагаем, что для k > 1 величина |W(Ωk)| пренебрежимо мала, что соответствует «гипотезе фильтра».

Если удовлетворяется «гипотеза фильтра», то приближённо можно записать

(6)

Отметим, что идеальный случай, когда |W(Ωk)|=0 при k>1, принципиально невозможен.

Подчеркнем, что в формуле (6) мы отбросили высшие гармоники не потому, что они малы, а потому, что их влияние на выходной сигнал системы пренебрежимо мало благодаря «гипотезе фильтра».

Таким образом, задача состоит в том, чтобы зная N(x) и W(p), вычислить числа А и Ω. Для решения этой задачи предварительно введем два важных понятия.