§4. Система управления с переменной структурой объектом второго порядка.

Покажем технику применения скользящих режимов на фазовой плоскости на примере системы второго порядка, относящейся к так называемому классу систем с переменной структурой. Этот класс систем был разработан коллективом ученых под руководством С.В.Емельянова в конце 60-х годов.

Предположим, что объект управления имеет передаточную функцию

(1)

Коэффициенты передаточной функции b и с могут изменяться в процессе работы, принимая, в том числе, и отрицательные значения. Известно только, что по модулю они ограничены некоторой величиной d. Рассмотрим способ построения системы стабилизации такого объекта, т.е. задача состоит в том, чтобы при любом начальном положении фазовых координат объекта выход системы возвращался в исходное положение равновесия.

Для решения поставленной задачи используем систему, структурная схема которой приведена на рисунке 1.

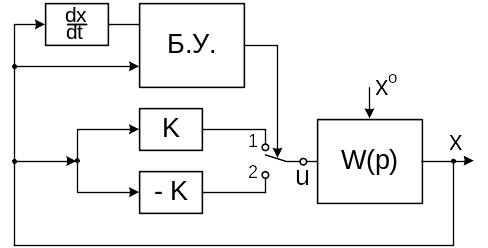
Рис. 1

Система работает следующим образом. В зависимости от величины изображающей точки на фазовой плоскости xy (y = x’) блок управления соединяет вход системы (координата u) или с точкой 1 или с точкой 2. В результате система на рисунке 1 преобразуется в одну из линейных систем, показанных на рисунках 2 и 3.

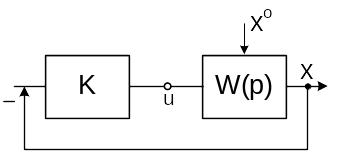
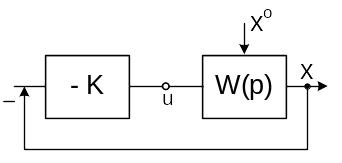
Рис. 2 Рис. 3

Характеристическое уравнение для структуры, изображённой на рисунке 2, имеет вид:

(2)

Величину k выбирают из условия, чтобы она была значительно больше d. Корни характеристического уравнения (2):

p_1,2= (3)

Характеристическое уравнение для структуры, изображённой на рисунке 4, имеет вид:

(4)

Корни характеристического уравнения (4):

p_1,2= (5)

Корни уравнения (3) являются комплексными (устойчивыми или неустойчивыми в зависимости от знака коэффициента b), а корни уравнения (5) являются действительными и разного знака. Эти утверждения следуют из того, что величина k выбирается значительно больше, чем модуль коэффициентов b и с. Поэтому можно приближённо записать:

(6)

(7)

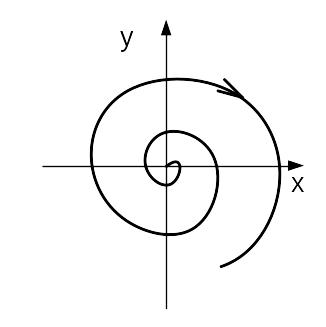
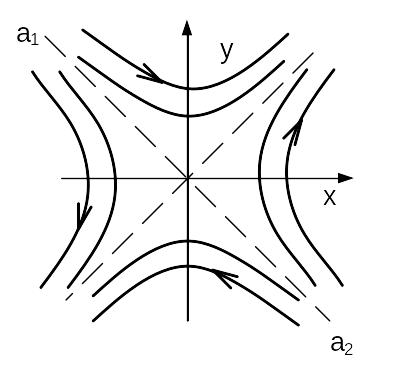
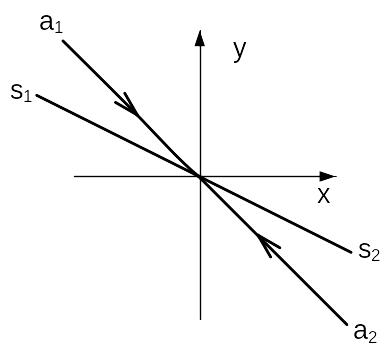
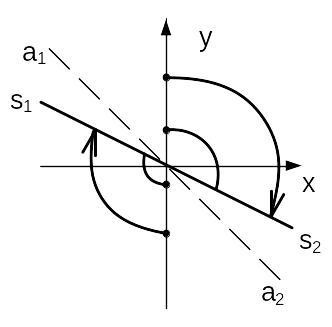
Таким образом, структура на рисунке 2 имеет особую точку типа «фокус» (устойчивую или неустойчивую, в зависимости от знака коэффициента b). А структура на рисунке 3 имеет особую точку типа «седло». На рисунках 4 и 5 приведены фазовые портреты для неустойчивого фокуса и узла. При этом в случае «узла» обозначена асимптота траектории, соответствующая устойчивому корню узла. К примеру, если характеристическое уравнение (4) имеет действительные корни –α и +β (α,β>0), то уравнение асимптоты а₁а₂ имеет вид:

y = -αx (8)

Проведем на плоскости линию S₁S₂, имеющую равнение y = λx. Величина λ выбирается таким образом, чтобы при любом допустимом значении α линии а₁а₂ и S₁S₂ располагались, как показано на рисунке 6.

Рис.4	Рис.5
Рис. 6	Рис. 7

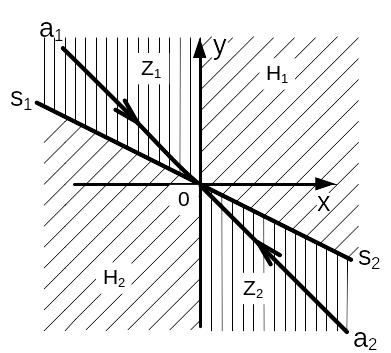
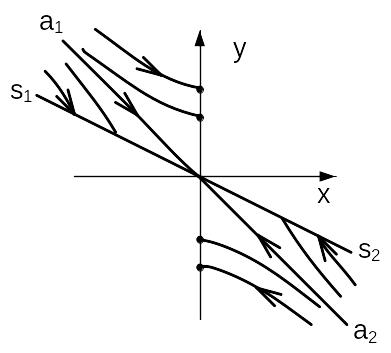
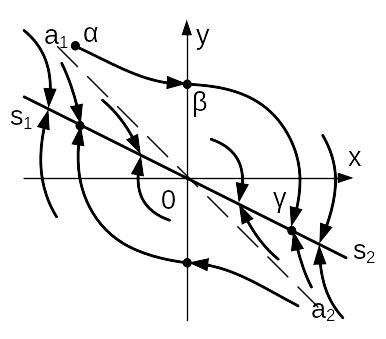
Блок управления разбивает фазовую плоскость на области. Первая область - Z₁Z₂, вторая область – Н₁Н₂, как показано на рисунке 7. Если изображающая точка находится в области Z₁Z₂, то включается система, изображенная на рисунке 2, и точка движется по соответствующей ветви гиперболы (седла), как показано на рисунке 9, до попадания на одну из границ области. Если изображающая точка находится в области Н₁Н₂, то включается система, изображенная на рисунке 3., и изображающая точка движется по спирали устойчивого или неустойчивого фокуса пока не выйдет на границу области (рис. 8).

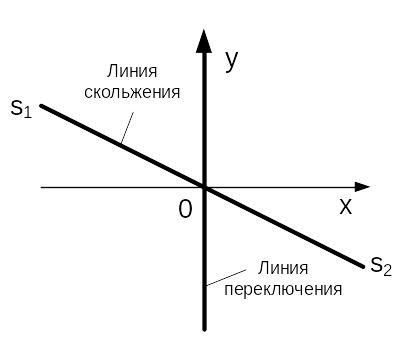
Как видно из рисунка 10, изображающая точка, попав на линию S₁S₂, не может с нее сойти, т.к. все траектории острием упираются в линию S₁S₂.

Изображающая точка движется по этой линии к началу координат в соответствии с дифференциальным уравнением

(9)

Линия S₁S₂ называется линией скольжения, а уравнение (9) – уравнением скольжения.

На рисунке 11 показано разбиение фазовой плоскости, которое использует регулятор при стабилизации объекта.

Рис.8	Рис.9
Рис.10	Рис.11

Замечание.

Обратим внимание, что одна из двух линейных структур, показанных на рисунках 2 и 3, заведомо неустойчива (это структура 3), а другая структура (показанная на рисунке 2) может быть устойчивой и может быть неустойчивой в зависимости от знака коэффициента b. Однако, исходная система, получаемая в результате переключения с одной структуры на другую, является устойчивой. Отсюда ясно происхождение названия – «система с переменной структурой».