2. Определение основных параметров системы

Процесс проектирования начинается с определения основных параметров будущей системы. Очевидно, что состав параметров систем управления оборудованием и исполнительных систем производства (систем обработки информации) существенно различается. В таблице 2.1 приведены примерные перечни задач, которые необходимо решить на этом этапе проектирования. Рекомендации о порядке решения этих задач при разработке различных систем приводятся ниже.

Таблица 2.1

Содержание второго раздела проекта
Система управления оборудованием технологического уровня	Определение длительности рабочего цикла системы Расчеты точности и быстродействия измерительно-преобразовательных каналов Расчет динамических параметров исполнительных устройств
Автоматизированная исполнительная система производства	Разработка модели предметной области: Разработка диаграммы Use Case для моделирования вариантов использования Разработка спецификаций функций для каждого варианта использования

2.1 Рекомендации по определению параметров системы управления технологическим оборудованием

При разработке проекта следует учитывать два наиболее важных свойства иерархической системы:

1. Свойство приоритетов – в иерархической системе команды верхнего уровня обязательны для выполнения нижестоящим уровнем.

2. Свойство взаимозависимости – функциональные возможности и характеристики нижестоящего уровня должны быть соизмеримы с заданиями и командами вышестоящего уровня.

Учет этих свойств требуют сосредоточить внимание, в первую очередь, на нижнем уровне, так как именно здесь формируются динамические характеристики системы и её точность.

Расчет длительности рабочего цикла программы

Длительность рабочего цикла пользовательской программы системы управления зависит от скорости изменения технологического параметра, которым управляет система, и допустимой ошибки управления. Чем выше скорость изменения технологического параметра, тем меньше должно быть значение длительности рабочего цикла выполнения пользовательской программы. Поэтому при управлении, например, тепловым процессом, где регулируется температура нагрева, время рабочего цикла может составлять единицы секунд, а при управлении процессом с высокой динамикой, например, приводом подачи станка с ЧПУ, рабочий цикл обычно имеет длительность 0,1-10 мс.

Если исполнительное устройство работает в условиях слабой динамики, например, привод робокара, то расчет длительности рабочего цикла ведется по формуле:

(2.1)

где – скоростная ошибка при максимальной скорости движения по координате; – допускаемая величина ускорения в м/с².

Если же исполнительное устройство работает в условиях высоких требований к динамике, то расчет длительности рабочего цикла программы управления следует вести с учетом обеспечения требуемой полосы частот системы управления.

На рисунке 2.1 изображена типичная форма желаемой логарифмической амплитудно-частотной характеристики (ЛАЧХ) цифровой системы управления скоростью.

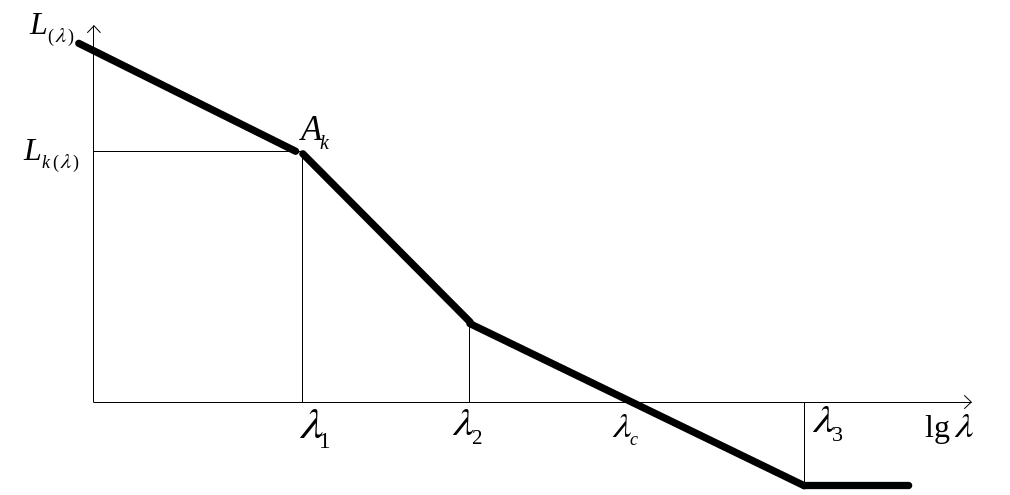
Рисунок 2.1 – Желаемая форма ЛАЧХ ЦСУ

Приведенная форма ЛАЧХ имеет следующие особенности:

• возможность устранить позиционную ошибку координатного движения – первая асимптота имеет наклон к оси частот 20 дБ/дек;

• ограничение скоростной ошибки – первая асимптота должна занять определенное положение на оси относительной амплитуды ;

• обеспечение устойчивой работы СУ – ЛАЧХ системы пересекает ось частот асимптотой с наклоном 20 дБ/дек;

• обеспечение требуемой полосы частот и показателя колебательности М – задается определенная длина асимптоты в частотном диапазоне .

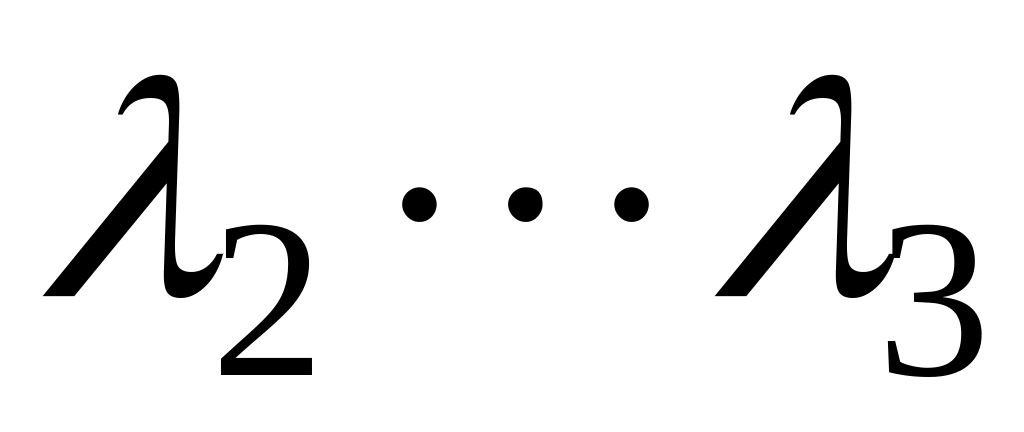Для приведенной выше формы желаемая ЛАЧХ описывается дискретной частотной характеристикой (ДЧХ):

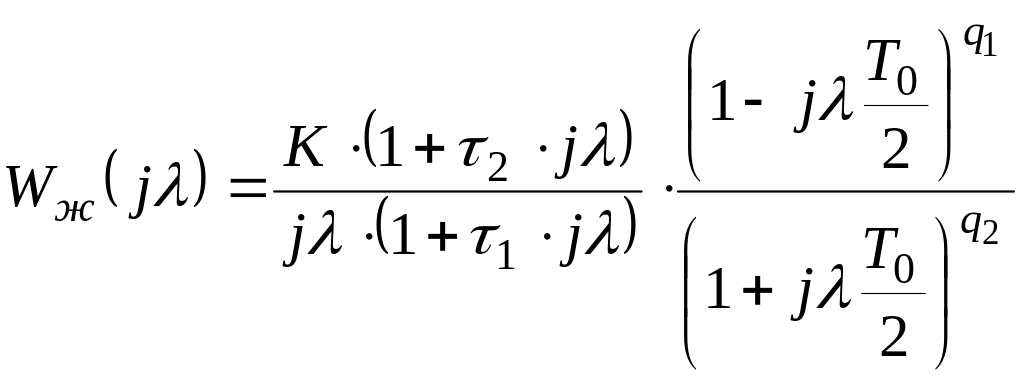, (2.2)

где – псевдочастота; ; ; ; – основные параметры, определяемые требованиями к системе управления; 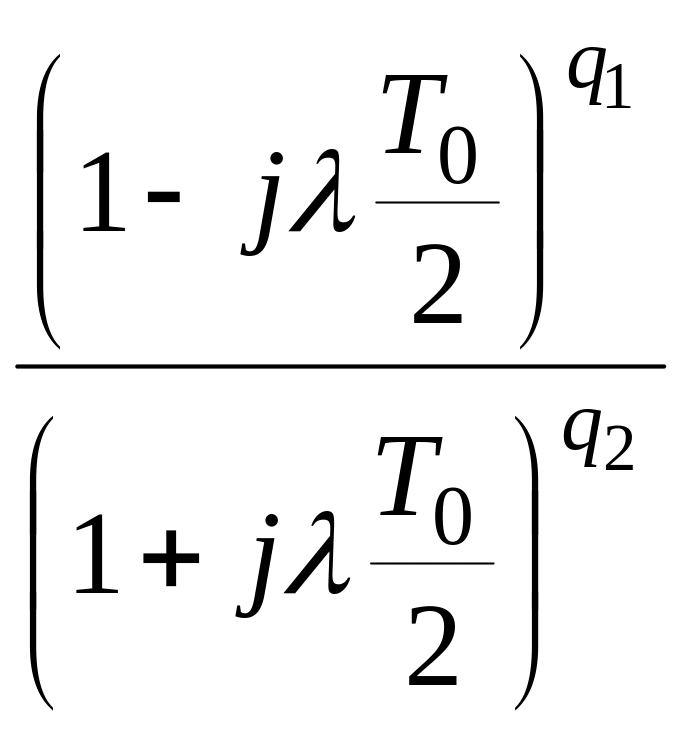– характеристика запаздывания.

Для определения основных параметров ДЧХ необходимо преобразовать заданные параметры технологического процесса (максимальную скорость и допускаемое ускорение ) в эквивалентные параметры гармонического сигнала (амплитуду и частоту ), а затем определить положение критической точки запретной области ЛАЧХ.

Преобразование параметров позволяет представить траекторию движения в виде функции, которая характерна для движения инструмента, например, фрезы по круговой траектории:

, (2.3)

где – текущее значение координаты; – амплитуда, радиус кругового контура; – угловая скорость движения.

Первая и вторая производные (скорость и ускорение) гармонического сигнала определяются известными выражениями:

, ,

где индексы обозначают максимальные (допускаемые) значения.

Отсюда можно определить эквивалентные параметры гармонического движения – частоту и амплитуду :

, .

Для низкочастотного участка ЛАЧХ справедливо допущение .

Тогда:

. (2.4)

Если известно значение ошибки , то должно быть выполнено условие:

(2.5)

Для относительной амплитуды это условие запишется в следующем виде:

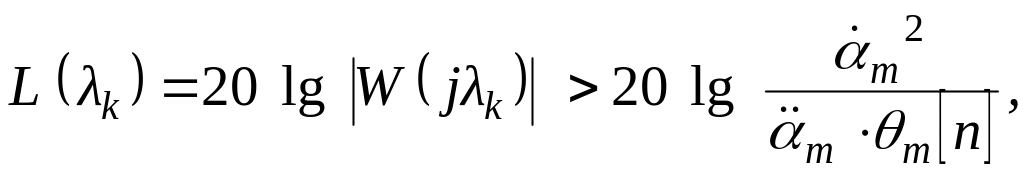(2.6)

В системах управления значения максимальной скорости , допускаемого ускорения и допускаемой скоростной ошибки должны быть известны.

Тогда, учитывая условия преобразования, для обеспечения необходимой точности желаемая ЛАЧХ должна проходить выше критической точки с координатами:

; (2.7) . (2.8)

При этом запретная область ограничивается по скорости первой асимптотой, которая проводится влево от точки с наклоном -20 дБ/дек. По ускорению эта запретная область ограничивается второй асимптотой, которая проводится вправо от точки с наклоном -40 дБ/дек. Положение запретной области показано на рисунке 2.2.

Скоростная ошибка и соответствующая ей максимальная скорость определяет необходимую добротность системы по скорости :

. (2.9)

Значение соответствует точке пересечения с осью линии, которая продолжает первую низкочастотную асимптоту (рис. 2.2).

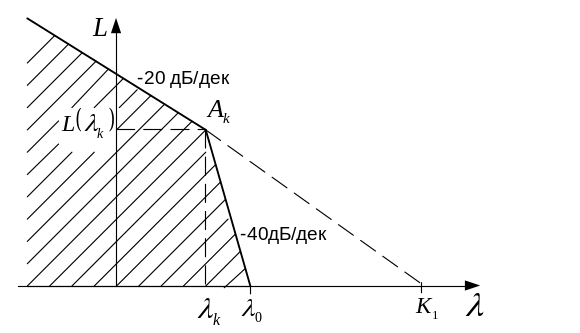
Рисунок 2.2 – Построение запретной области по критерию точности

При построении следует придерживаться следующего порядка.

1. Первая низкочастотная асимптота желаемой ЛАХ проводится с наклоном –20 дБ/дек выше точки 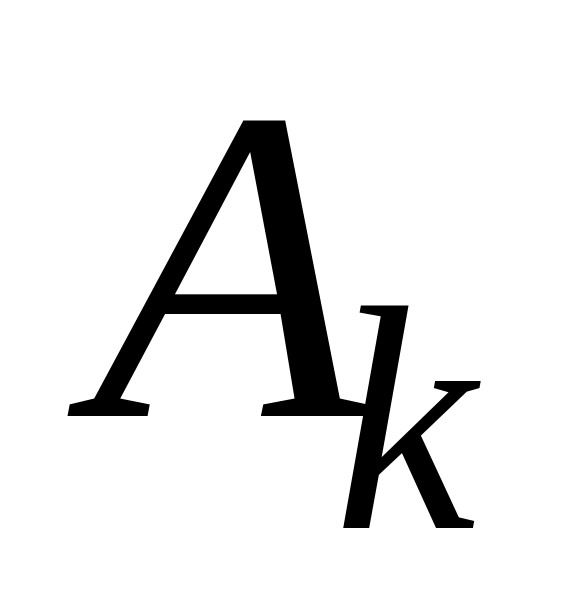на 3 дБ, чтобы обеспечить запас устойчивости. Подъем характеристики приводит к увеличению коэффициента добротности по скорости в 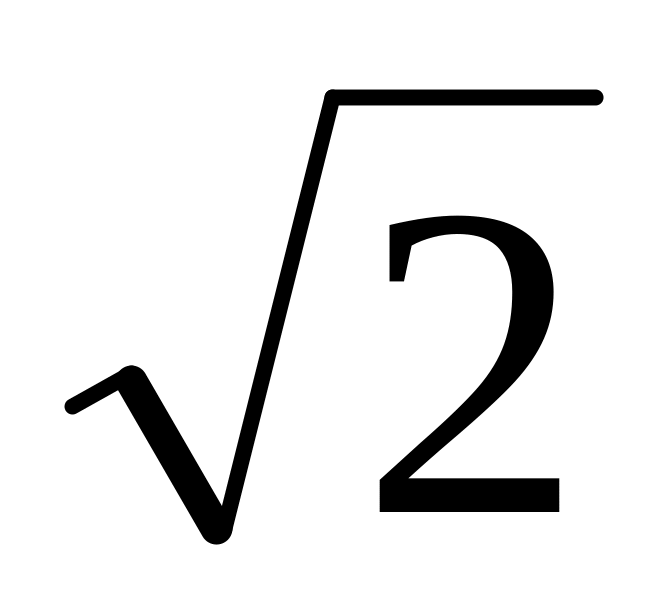раза:

. (2.10)

2. Вторая асимптота проводится с наклоном –40 дБ/дек от точки сопряжения с координатами ( 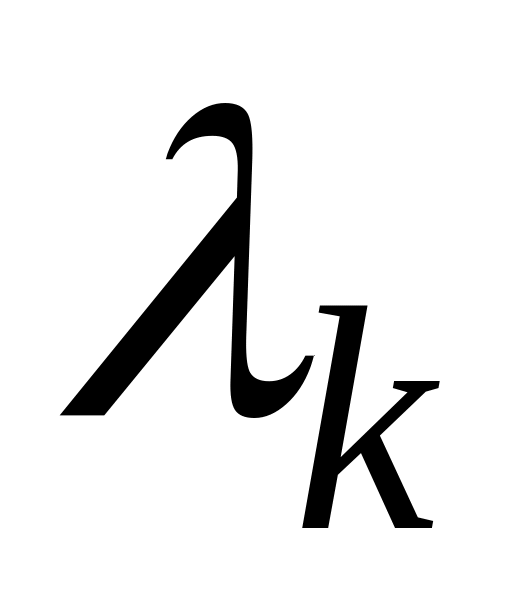; 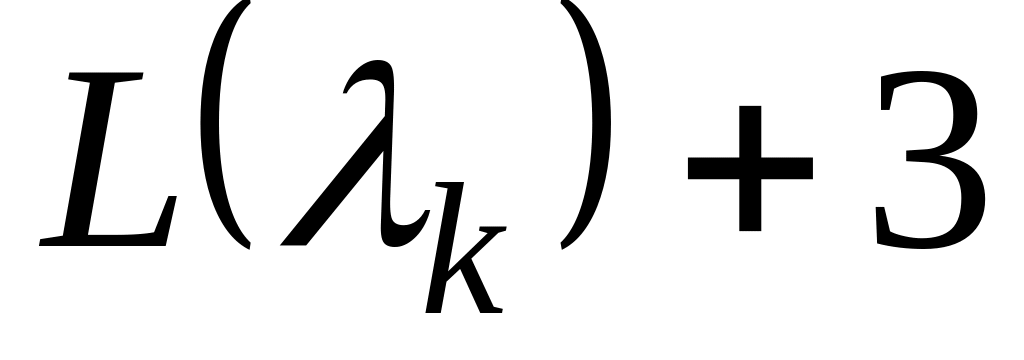) до точки пересечения с осью , которая определяет базовую частоту 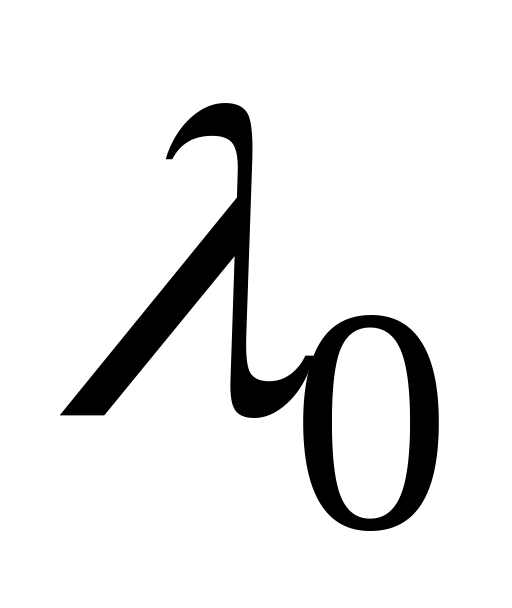запретной области:

. (2.11)

3. По заданному показателю колебательности 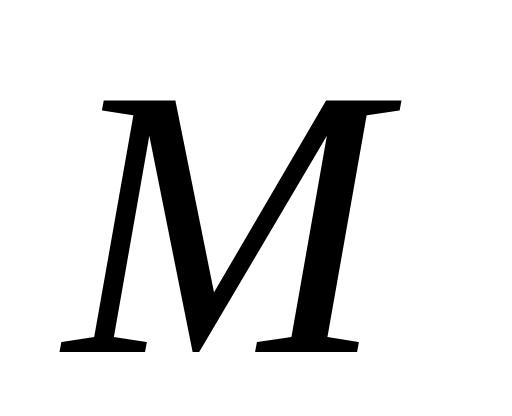(обычно М=1,2…1,7) определяется частота сопряжения второй и третьей асимптот:

. (2.12)

3. Третья асимптота с наклоном –20 дБ/дек проводится от точки 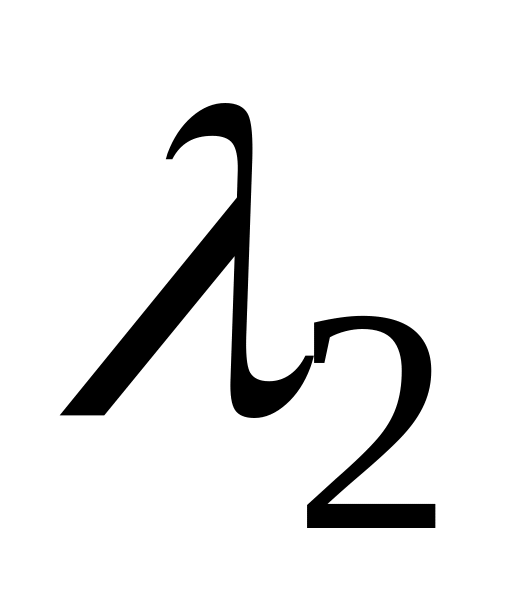до точки 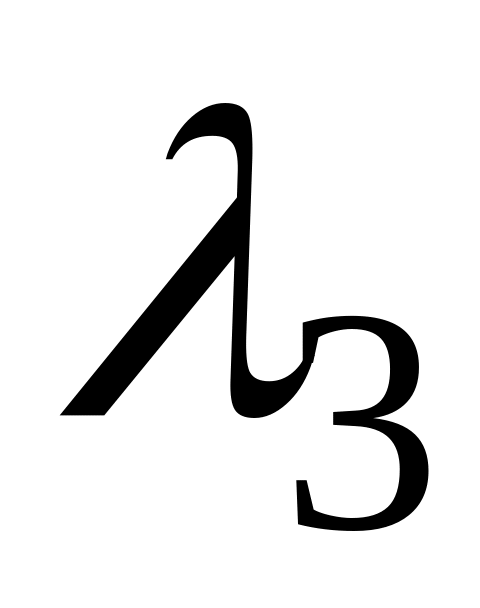, которая также зависит от показателя колебательности:

. (2.13)

Четвертая асимптота в цифровых системах управления проводится параллельно оси частот.

Окончательный вид логарифмической частотной характеристики представлен на рис. 2.3.

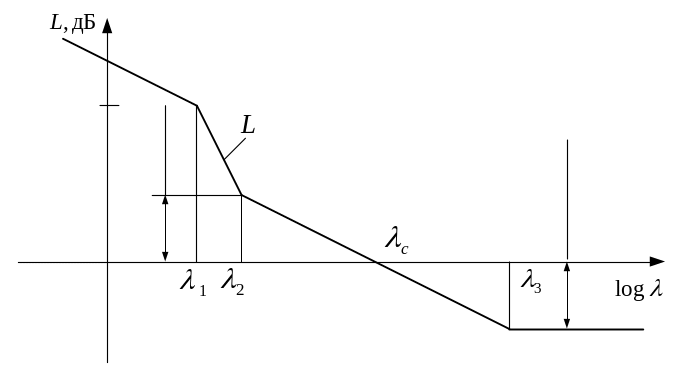
Рисунок 2.3 – Окончательный вид ЛАЧХ для проектируемой СУ

В верхнем диапазоне частота определяется значением периода дискретности :

.

При выборе периода дискретности следует руководствоваться выражением:

. (2.14)

В последующих расчетах должно быть принято такое значение , которое удовлетворяет условию (2.14).

Расчет точности и быстродействия измерительных каналов

Определение разрядности АЦП или ЦАП производится из условия обеспечения точности преобразования.

Величина ошибки преобразования зависит от скорости изменения сигнала на входе АЦП или на выходе ЦАП.

Для гармонического сигнала :

(2.15)

значение ошибки определяется из неравенства:

. (2.16)

Определим ошибку для конкретного примера. Пусть , , . Тогда ошибка составит:

.

Как видно из примера, даже при небольших значениях частоты сигнала значение ошибки составляет 20% от уровня сигнала, что во многих случаях недопустимо. При увеличении частоты сигнала это значение будет увеличиваться пропорционально. Единственным способом уменьшения ошибки является уменьшение периода дискретизации непрерывного сигнала, то есть длительности рабочего цикла системы управления. Так, например, в системе регулирования выходного тока частотного преобразователя для обеспечения требуемой точности дискретность должна быть на уровне 2 мкс при верхнем уровне частоты выходного напряжения преобразователя 400-600 Гц, что соответствует угловой скорости .

Однако ошибка дискретизации – это не единственная составляющая погрешности преобразования. Второй составляющей этой погрешности является разрешающая способность, или абсолютная ошибка преобразователя. Обычно она принимается равной цене одной дискреты, то есть 1 в младшем разряде кода.

Для выбора разрядности кода и, следовательно, разрешающей способности используется такая характеристика, как динамический диапазон.

Пример. Необходимо выбрать разрядность ЦАП для подачи сигнала на аналоговый регулятор тока, обеспечивающий изменение тока от 0 до 600 А с точностью 2 А. Тогда динамический диапазон буде равен:

.

Отсюда требуемая разрядность ЦАП (число разрядов) определяется целым числом ent (фр. антье):

,

где дополнительная 1 означает замену дробной части целым.

Для приведенного выше примера требуемая разрядность ЦАП равна:

(разрядов).

Таким же образом определяется и разрядность АЦП.

Пример. Пусть аналоговый сигнал некоторого измерительного преобразователя изменяется в пределах ±5 В. Требуемая точность его представления должна составлять не более 1мВ. Тогда динамический диапазон будет равен отношению двойной амплитуды к точности её представления:

.

Количество разрядов АЦП, необходимое для такого представления, равно:

Параметры быстродействия АЦП и ЦАП важно учитывать всегда, особенно, когда в системе существует несколько каналов аналоговых вводов и аналоговых выводов. В большей мере это важно для каналов ввода, поскольку время преобразования в АЦП значительно больше времени преобразования в ЦАП. Проблема заключается в том, что каналы (группы каналов) включаются последовательно и общее время обслуживания каналов (время цикла) зависит от количества каналов и групп каналов.

На рис. 2.4 показана временная диаграмма обработки сигналов для модуля SM 331 AI 8×14 bit High Speed, который имеет наиболее высокое быстродействие – время преобразования одного канала составляет 52 мкс, а разрешение модуля (время его обработки) – 625 мкс.

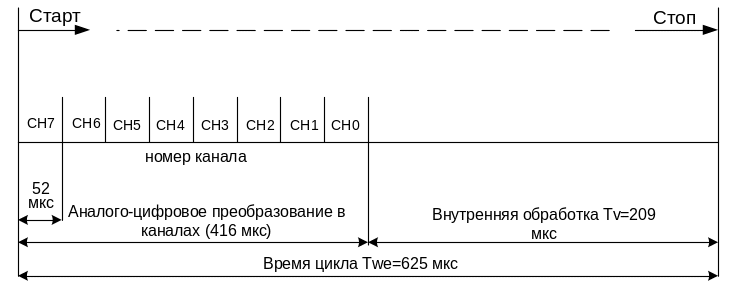
Рисунок 2.4 – Временная диаграмма обработки данных в модуле аналогового ввода SM 331 AI 8×14 bit High Speed

Для менее динамичных процессов следует применять обычные модули ввода, например, SM 331 AI 8×12 bit, у которого время преобразования канала составляет 100 мс, а время разрешения модуля около 1200 мс.

Для обслуживания таких модулей необходимо организовать соответствующее время цикла или вводить аппаратное прерывание при готовности модуля передать новые данные.

Расчет динамических параметров исполнительных устройств

Исполнительные устройства системы управления, по сути, представляют собой фильтр нижних частот. Параметры такого фильтра следует выбирать так, чтобы они не «обрезали» желаемую частотную характеристику системы управления.

Динамические параметры исполнительных устройств во многом зависят от их мощности – с увеличением мощности обычно возрастают массогабаритные характеристики и моменты инерции. Кроме того, динамические характеристики зависят от конструктивных особенностей исполнительного устройства.

Эти обстоятельства создают проектировщику определенные проблемы, для разрешения которых разрабатываются комплексные мероприятия. Так, например, для удовлетворения высоких требований к динамике в системах управления приводами подач станков с ЧПУ необходимо стремиться к минимальной длине кинематической цепи, исключать упругие элементы, применять двигатели с наименьшими массоразмерными характеристиками, высокими показателями перегрузочной способности, минимальным моментом инерции якоря, а также минимальными значениями постоянных времени.

В процессе проектирования следует применять те методики расчетов, которые приняты как стандартные. Так, например, для расчетов электроприводов станков с ЧПУ следует применять стандартную методику, приведенную в [4].

Выполнение расчетов должно производиться с обязательным представлением расчетной схемы, на которой необходимо показать кинематическую схему привода, действующие нагрузки, размерные и кинематические характеристики.

Динамические свойства исполнительных устройств характеризуются постоянными времени отдельных звеньев. Общее значение постоянной времени исполнительного устройства можно получить либо путем расчета, используя математическое описание исполнительного устройства, либо путем моделирования в программной среде Simulink.