2.5. Модели роста, учитывающие затраты на поддержание жизнедеятельности

Влияние процессов поддержания жизнедеятельности на рост микроорганизмов описывается двумя моделями: «энергии поддержания» и «эндогенного дыхания». Первая из них, предложенная Пертом, получила экспериментальное подтверждение и широко применяется в микробиологии. Вторая была разработана Гербертом для объяснения снижения прироста биомассы в процессе биологической очистки активным илом.

Согласно модели «энергии поддержания» внеклеточный субстрат используется клетками в двух направлениях: на рост и получение энергии поддержания жизнедеятельности:

Соответственно, общее количество потребленного субстрата представляется в виде суммы затрат на рост и поддержание жизнедеятельности :

. (2.22)

Принимается, что затраты субстрата на поддержание жизнедеятельности пропорциональны концентрации биомассы:

, (2.23)

где  коэффициент энергии поддержания (удельная скорость потребления субстрата на поддержание жизнедеятельности).

Вводится истинный экономический коэффициент , равный экономическому коэффициенту при нулевых затратах субстрата на поддержание жизнедеятельности:

, (2.24)

. (2.25)

При аэробном росте гетеротрофов на простых органических субстратах (сахара, органические кислоты) в оптимальных условиях =0,45 г/гХПК.

Из соотношений (2.22)-(2.25) вытекает зависимость экономического коэффициента от удельной скорости роста:

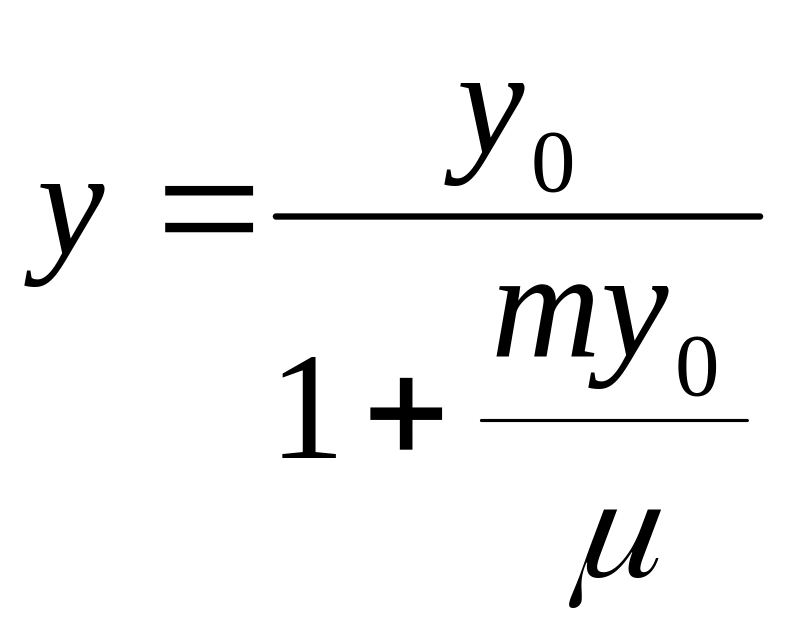, (2.26)

. (2.27)

Потребление кислорода аэробными гетеротрофами описывается аналогичными уравнениями:

, (2.28)

, (2.29)

, (2.30)

где ,  количество кислорода, потребленного на рост и поддержание жизнедеятельности;  истинный энергетический коэффициент ( =0,4 гО₂/гХПК);  удельная скорость потребления кислорода на процессы поддержания жизнедеятельности.

Если концентрация органического субстрата измеряется в кислородных единицах (по ХПК), то с учетом (2.6) выполняется:

; , (2.31)

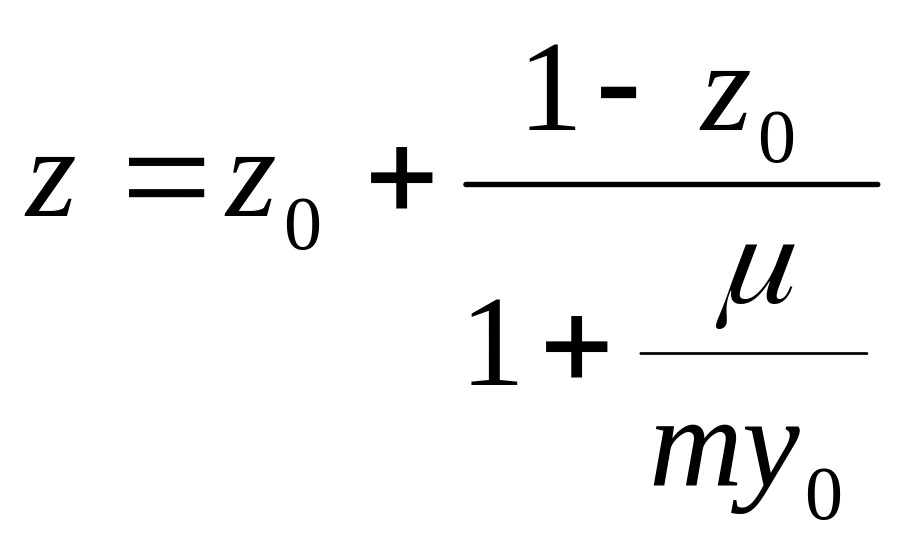. (2.32)

Модель эндогенного дыхания постулирует, что энергия поддержания жизнедеятельности образуется в результате самоокисления биомассы по схеме:

Основные уравнения этой модели имеют вид:

, (2.33)

, (2.34)

где  константа скорости самоокисления биомассы;  удельная скорость эндогенного дыхания (удельная скорость потребления кислорода на самоокисление биомассы для получения энергии на по

Из (2.33), (2.34) следует:

, (2.35)

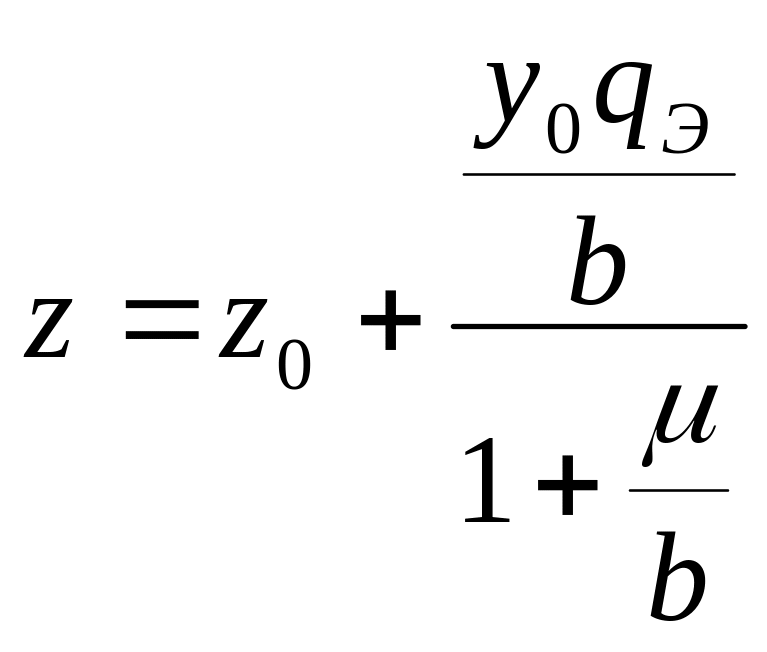. (2.36)

Из сопоставления уравнений (2.26), (2.32) и (2.35), (2.36) видно, что обе модели дают одинаковые результаты при , , где  кислородный эквивалент биомассы.

Зависимость коэффициентов и от удельной скорости роста показана на рис. 2.6. Для экспериментального определения параметров модели можно использовать линеаризованную форму (2.27).

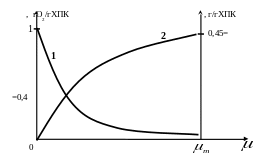
Рис. 2.6. Зависимость энергетического коэффициента (1) и экономического коэффициента (2) от удельной скорости роста

Для бактерий =0,001-0,1 ч^-1. Поэтому при , когда выполняется: , . Но в условиях лимитирования роста ( , ) экономический коэффициент существенно ниже истинного значения ( ), соответственно . Такая система типична для систем биологической очистки, задачей которых является снижение до минимума содержания органических веществ в воде ( ).

Рассмотренные модели позволяют уточнить уравнение Моно. Из (2.22)-(2.25) и (2.33) в совокупности с уравнением (2.8) следует:

(2.37)

или

. (2.38)

Уравнения (2.37), (2.38) отражают тот факт, что рост микроорганизмов возможен лишь при концентрации субстрата выше некоторой минимальной величины . При весь внеклеточный субстрат расходуется на поддержание жизнедеятельности и клетки не растут, а напротив, вынуждены окислять свои резервы, соответственно .

Величину легко найти из уравнений (2.37), (2.38) при =0:

. (2.39)

Так как ( ), то в первом приближении получим:

. (2.40)

Отсюда следует:

.

Так как для органических субстратов =1-10 мг/л, то составляет всего 0,01-0,1 мг/л. Однако при лимитировании роста по диффузии субстрата величина может быть значительно больше (до нескольких мг/л) и в соответствии с (2.13) определяется по формуле:

, (2.41)

где задается уравнением (2.14).