16.Осевые моменты инерции тел простейшей формы.

l

Осевые моменты инерции однородных тел простой формы.

l/2

1. Стержень

y₁

y

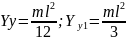
y

z

2. Круговой диск

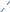
Y_x = Y_y = 1/4mR²

Y_z = 1/2mR²

z

3. Сплошного кругового цилиндра:

R

H

Y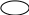_x = Y_y = n(1/4P_i² + 1/12H²)

y

Y_z = 1/2mR²

x

4. Шар - Y_x = Y_y = Y_z = 2/5mR²

12. Некоторые основные понятия динамики системы материальных точек (система материальных точек, связи, силы).

Некоторые основные понятия динамики.

Системы материальных точек.

Система материальных точек – такая их совокупность которых положение и движение отдельных точек взаимосвязаны и взаимозависимы.

Связи – это тело, ограничивающее движение материальной точки.

Механическая сила – это мера механического взаимодействия систем материальных точек.

Сила внешняя и внутренняя:

F^e – внешняя сила – это силы, действующие на точку системы со стороны тел не входящих в систему.

Fⁱ – внутренние силы – это силы, вызванные взаимодействием точек, входящих в систему.

18. Теорема о движении центра масс механической системы. Закон сохранения.

Теорема о движении центра масс системы.

При движении механической системы в любой момент времени произведение массы системы на ускорение её центра масс равно геометрической сумме всех действующих на систему внешних сил.

Ма_с - ∑F_c

Законы сохранения движения центра масс.

Если векторная сумма всех внешних сил действующих на систему ровна нулю, то центр масс действующих на систему находится в покое или совершает равномерное прямолинейное движение.

∑F^e = 0, то Ma_c = 0

a_c = 0 => ϑ_c = const

Количество движения – это векторная величина характеризующая динамические свойства материальных точек определяется по формуле:

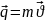
20. Теорема о изменении количества движения механической системы. Привести пример.

Теорема об изменении колличества движения механической системы.

1. При движении механической системы быстрота изменений её количества движения ровна векторной сумме всех внешних сил действующих на систему: dQ/dt = ∑F_i^e

2. В интегральной форме:

При перемещении механической системы изменения её количества движения ровно сумме импульсов внешних сил, действующих на систему за время движения: Q₁ – Q₀ = ∑S_i^e

Закон сохранения количества движения.

Если векторная сумма всех внешних сил действующих на систему ровна нулю, то вектор количества движения этой системы постоянно по модулю и направлению: если ∑F_i^e = 0, то Q = const.

22. Теорема об изменении главного момента количества движения механичческой системы

Теорема об изменении момента количества движения системы.

При движении механической системы быстрота изменения её момента количества движения в любой момент времени относительно некоторого неподвижного центра геометрически ровна сумме моментов внешних сил, действующих на эту систему относительно того же центра.