3.Первая основная задача динамики точки и ее решение.

Первая основная задача динамики точки.

Эта задача, в которой известны масса точки и кинематическое уравнение движения точки.

Необходимо определить действуюшюю на её силы. Решается в зависимости от способа заданного движения.

Рассмотрим для координатного способа:

1. 

2)Подставляем диф. уравнение

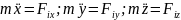
3)Вычисляем внешние силы

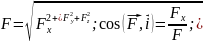
37.Понятие о принципе Даламбера. Принцип Даламбера для материальной точки.

Принцип Даламбера:

Общий принцип механики, при помощи которого уравнение динамики придаётся вид – уравнение статики.

R

Рассмотрим движущуюся несвободную материальную точку:

F

R – реакции;

Q

F – задаваемые внешние силы Q – ускорение.

Согласно основному уравнению динамики:

ma - ∑Fi; ma = F + R; F + R – ma = 0; F + R + Ф = 0

где Ф = -ma – сила энергии материальной точки (Даламбера сила)

Принцип Даламбера для материал. точки :

В любой момент времени векторная сумма задоваемых внешних сил, сил инерции и реакции ровна нулю.

Векторное уравнению F + R + Ф = 0, как и в стакане соответствуют 3 уравнения проекции на оси координат.

13. Маса и центр масс системы материальных точек.

Система материальных точек – такая их совокупность которых положение и движение отдельных точек взаимосвязаны и взаимозависимы.

Масса механической системы – это сколярная величина, равная арефмитической сумме масс всех точек входящих в систему: М = ∑mi

Центр масс механической системы – это центр паралельных сил, сообщающих точкам системы одинаковые ускорения.

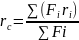
Центр масс системы геометрически совпадает с центром тяжести.

14.Момент инерции тела. Радиус инерции.

Момент инерции тела относительно оси (осевой момент инерции).

Это сколярная величина, равная арефмитической сумме произведения масс всех точек на квадраты расстояния до оси:

Y_x = ∑m_i*r_xi²; r_xi² = y_i² + z_i²

Y_y = ∑m_i*r_yi²; r_yi² = x_i² + z_i²

Y_z = ∑m_i*r_zi²; r_xi² = x_i² + y_i²

Ось координат проведённый через центр масс тела наз. центральной осью его инерции.

21. Момент количества движения материальной точки и механической системы. Привести приемер

Момент количества движения механической системы относительно произвольного центра О.

Наз. величина равное геометрической сумме момента количества движения всех точек системы относительно центра О. L₀ = ∑(r_i*q_i) = ∑(r_i*m_iϑ_i)

F

Величина момента количества движения точки вычисляются так же как и величина момента силы при этом сохраняется то же правило знаков.

h

М0(F) = ±F*h

0

L0 = ±q*h

Частные случаи вычисления моментов колич. движение.

1. Тело совершает криволинейное поступательное движение: L₀ = ±m*ϑ_c*h_c

2. Тело совершает вращательное движение вокруг неподвижной оси: L_oz = ±Y_zω

Тело совершает плоское движение: L_oz = ±mϑ_c * h_c ±Y_z*ω