4.Вторая основная задача динамики точки и ее решение.

Вторая основная задача динамики точки.

Эта задача, в которой известна масса точки и силы действующие на точку, а также начальное условие движения точки. Необходимо определить кинемотическое уравнение движение точки.

Ход решения для прямолинейного движения точки:

Дважды интегрируя его, находим общее решение: x = f(t₁,c₁,c₂), их находим из начального условия: t = 0, x = x₀, V_x = x = V₀.Частное решение имеет вид: x = f(t, x₀, V₀)

9.Вынужденные колебания точки при наличии сопротивления окружающей среды.

1. Вынужденные колебания точки при наличие сопротивления среды.

2. - Такие колебания возникают под действием гармонической силы Q при сопротивлении среды

   

   Q

   F

   R

3. .

   

4. 

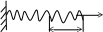
   Mo

   x

   M

7. F = c*x – восстановленная сила R = Mϑ = μx – сила сопротивления среды.

8. Q = Q_osinpt – внешняя гормональная сила

6.Виды колебаний точки. Свободные колебания.

Колебания материальной точки.

Колебания точки и систем очень распростронены в технике, в одних случаях они используются для создания объекта, а в других представляют опастность вдля объектов техники.

В последнем случае необходимо конструировать средства гашения колебаний.

Колебания точки бывают:

1. линейные и нелинейные

2. большие и малые

Линейные бывают:

- свободные

- затухающие

- вынужденные

Свободные колебания точки

Если движение точки происходит без сопротивления (учета сопротивления среды), то колебания называются свободными(собственными).

Рассмотрим модель механических свободных колебаний.

Она представляет собой консольный стержень, на который одета пружина с шариком на конце. Если шарик оттянуть вправо на расстоянии х, то на него будет действовать сила со стороны пружины F, её называют восстанавливающей силой.

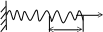
х

М₀ х М

F = c*x где с – жесткость пружины

- частота свободных коллебаний

x+k²x = 0 - даф. уравнение свободных колебаний.

x = Asin(kt+α₀) – кинематическое уравнение свободных колебаний.

Т

А

А – амплитуда колебаний (это модуль наибольшего смещения тела от положения равновесия)

Т – период колебания (минимальный промежуток времени по истечению которого повторяются значения всех величин, характеризующих периодически колебательный процесс.

8.Вынужденные колебания точки при отсутствии сопротивления окружающей среды.

Вынужденные колебания точки при отсутствии сопротивления среды.

Такие колебания возникают под действием гармонической силы Q

Механическая модель:

F

Q

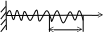
Mo

M

x

F = cx – восст. сила

Q = Qo*sinpt – внешняя гармоническая сила

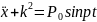– диф. уравнение при отсутствии сопротивл. среды

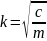– хор-ет вост. силы

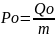– гармоническую силу.

1. Частота собственных колебаний точки не совпадает с возмущающей силой.

Кинематическое уравнение:

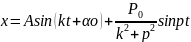
свободное вынужденное колеб. Точк.

x

Таким образом движение точки состоит из двух движений, т.е. метод суперпозициями (наложениями)

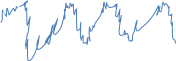
t

2. Частота собственных колебаний точки совпадает с возмущающей силой.

Кинематическое уравнение имеет вид:

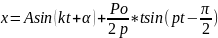
Во второе слагаемое входит время t – это означает, что вынужденные колебания при совподении частот p и k с течением времени неограниченно возростает, это явление в технике называют резонансом.

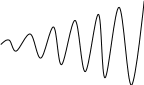
P₀/2p*t

x

t

P₀/2p*t