1.5. Приклад розрахунку

З продукції автомата, який оброблює ролики з діаметром D=20_-0,20 мм була взята партія об`ємом N=100 штук. Ролики були заміряні по діаметру мікрометром з ціною поділки 0,01 мм. Відхилення діаметрів роликів від номіналу представлені в табл. 1.2.

Таблиця 1.2 - Відхилення діаметрів роликів від номінального значення

1	2	3	4	5	6	7	8	9	10
-0,07	-0,03	-0,04	-0,08	-0,03	-0,08	-0,09	-0,11	-0,11	-0,10
-0,14	-0,08	-0,06	-0,06	-0,04	-0,03	-0,04	-0,07	-0,11	-0,13
-0,03	-0,07	-0,08	-0,08	-0,05	-0,05	-0,07	-0,03	-0,09	-0,12
-0,05	-0,12	-0,07	-0,06	-0,11	-0,10	-0,12	-0,12	-0,03	-0,10
-0,08	-0,05	-0,11	0,07	-0,05	-0,08	-0,09	-0,09	-0,09	-0,02
-0,06	-0,13	-0,05	-0,07-	-0,11	-0,05	-0,08	-0,03	-0,11	-0,09
-0,11	-0,06	-0,07	-0,06	-0,06	-0,12	-0,10	-0,08	-0,09	-0,01
-0,05	-0,07	-0,06	-0,05	-0,10	-0,09	-0,04	-0,09	-0,08	-0,09
-0,07	-0,04	-0,06	-0,12	-0,05	-0,03	-0,10	-0,09	-0,09	-0,08
-0,08	-0,07	-0,07	-0,09	-0,08	-0,11	-0,10	-0,12	-0,10	-0,10

Згідно табл. 1.2 ∆Х_max=0,01 мм, ∆X_min=0,14 мм. Отже, величина емпіричного поля розсіювання розглянутої партії дорівнює:

W=−0,01−(−0,14)=0,13 мм.

Задамо число інтервалів К=7, визначимо ціну інтервалу С:

мм.

Відхилення між ∆X_max та ∆X_min разбиваються на 7 груп з інтервалом С=0,02 мм, та підраховується частота (m_i) поява відхилень в середині кожного інтервалу. Результати зведені до табл.1.3.

Таблиця 1.3 – Результати розбиття партії на групи

Інтервали від	Інтервали до	Середина інтервалу ∆Xj	Підрахунок частот	Частота
-0,14	-0,12	-0,13	ІІІ	3
-0,12	-0,10	-0,11	ІІІІІІІІІІІІІІІІ	16
-0,10	-0,08	-0,09	ІІІІІІІІІІІІІІІІІІІІІІ	22
-0,08	-0,06	-0,07	ІІІІІІІІІІІІІІІІІІІІІІІІІ	25
-0,06	-0,04	-0,05	ІІІІІІІІІІІІІІІІІІІ	19
-0,04	-0,02	-0,03	ІІІІІІІІІІІІІ	13
-0,02	0,00	-0,01	ІІ	2
100

Для розрахунку статистичних характеристик розподілення та можна використовувати формули (1.7) та (1.8) чи використовувати менш трудомісткий метод умовних одиниць, для чого складаємо допоміжну табл. 1.4.

Таблиця 1.4 – До розрахунку статистичних характеристик розподілу

Інтервали		Середина інтервала ∆Хj	Частота mj
від	до
-0,14	-0,12	-0,13	3	-3	-9	27
-0,12	-0,10	-0,11	16	-2	-32	64
-0,10	-0,08	-0,09	22	-1	-22	22
-0,08	-0,06	-0,07	25	0	0	0
-0,06	-0,04	-0,05	19	1	19	19
-0,04	-0,02	-0,03	13	2	26	62
-0,02	0,00	-0,01	2	3	6	18

Для заповнення графи 5 необхідно встановити значення „а”. Найкраще приймати „а” рівним ∆Х_j з найбільшою частотою, тобто в даному випадку а=−0,07.

Графа 6 − це добуток граф 4 та 5, а графа 7 − добуток граф 5 та 6.

Далі потрібно розрахувати суми за графами 4, 6, 7. Шукані значення та знаходять за наступними формулами:

;

.

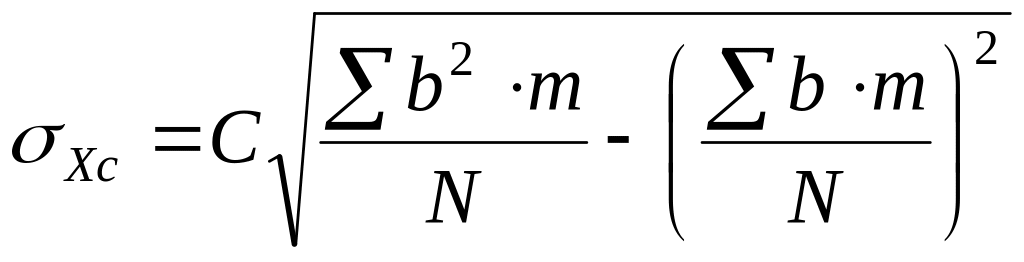При розрахунках приймаємо:

А=−0,07; С=0,02;

;

.

Для побудови кривої нормального розподілення визначаються наступні величини:

− максимальна ордината за формулою (1.11)

;

− ординати точок згину на відстані від (1.12)

;

− ординати на відстані від (1.13)

;

− ординати на відстані від (14)

;

− величина теоретичного поля розсіювання партії

.

За цими даними будується крива нормального розподілення безпосередньо на графіку розсіювання фактичних розмірів (на гістограмі) (рис. 1.4).

На графік наносять в прийнятому масштабі величину заданого поля допуску з граничними розмірами 20 мм та 19,8 мм, та через верхню та нижню межі поля допуску проводять ординати до перетину з кривою нормального розподілення.

Величина заштрихованої площі в межах поля допуску, віднесена до всієї площі кривої нормального розподілення, визначає ймовірність отримання деталей в межах допуску, а звідси випливає ймовірність отримання деталей, які виходять за межі поля допуску, тобто величини ймовірного браку.

Величина фактичного браку рівна кількості розмірів деталей партії які фактично вийшли за межі поля допуску чи їх величини в відсотках до загального об'єму партії.

Розрахунок ймовірного браку

Значення аргументів (Z) для верхньої (Z_в) та нижньої (Z_н) межі поля допуску

;

.

Величина отримання ймовірного браку Р (в %) рівна:

%;

%;