2.2 Побудова моделі за допомогою поліноміальної інтерполяції поліномом 7-го степеня

Побудова моделі за допомогою поліноміальної інтерполяції поліномом 7-го степеня виконуємо тим же способом як і для вхідного сигналу U(t), що описаний в другому розділі.

Нижче наведено лістинг програмного модуля в середовищі Matlab:

clear;

load data.mat

n=129;

for i=1:8;

for j=1:8;

A(i,j)=sum(n2t.^(i+j-2));

end;

end;

for i=1:8;

B(i)=sum(n2t.^(i-1).*n2wt);

end;

a=B/A;

t=1:150;

f=a(8)*t.^7+a(7)*t.^6+a(6)*t.^5+a(5)*t.^4+a(4)*t.^3+a(3)*t.^2+a(2)*t+a(1);

hPlot=plot(t,f);

hold on;

plot(n2t,n2wt,'red')

го степеня')

xlabel('t')

ylabel('W(t)')

axis([0,150,-0.5,6.5]);

set( hPlot, 'LineWidth', 2 );

Нижче наведемо графічну модель (рис. 2.1):

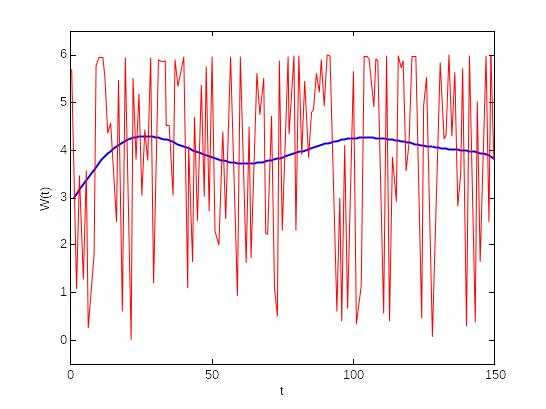
Рис. 2.1. Поліноміальна модель вхідного сигналу W(t) поліномом n-го порядку

Розв’язавши систему, отримаємо такі значення коефіцієнтів:

a₀ = 2.8984;

a₁ = 0.0876;

a₂ = 0.00081;

a₃ = -0.00023;

a₄ = 0.0000039;

a₅ = 0.000000041;

a₆ = 1.9851551e-010;

a₇ = -3.703921e-013.

2.3 Побудова моделі за допомогою полінома Чебишева

Побудова моделі за допомогою полінома Чебишева виконуємо тим же способом як і для вхідного сигналу U(t), що описаний в другому розділі.

Нижче наведено лістинг програмного модуля в середовищі Matlab:

clear;

load data.mat;

Cheb_por=7;

n=129;

fi=ones(n,7);

for i=1:n

fi(i,2)=n2t(i)-(1/n)*sum(n2t);

end;

for p=3:Cheb_por; i=1:n;

beta(p)=-sum(n2t(i).*fi(i,p-1).^2)/sum(fi(i,p-1).^2);

gama(p)=-sum(n2t(i).*fi(i,p-1).*fi(i,p-2))/sum(fi(i,p-1).^2);

fi(i,p)=(n2t(i)+beta(p)).*fi(i,p-1)+gama(p).*fi(i,p-2);

end;

A=fi'*fi;

B=fi'*n2wt;

a=A\B;

for i=1:n; j=1:7;

Cheb(i)=a(j)'*fi(i,j)';

end;

hPlot=plot(n2t,Cheb);

hold on;

plot(n2t,n2wt,'red');

xlabel('t');

ylabel('U(t)');

set( hPlot, 'LineWidth', 2 );

Нижче наведено модель досліджуваного об’єкта (рис. 2.2).

Розв’язавши систему, отримаємо такі значення коефіцієнтів:

a₀ = 4.1045; a₆ = 3.69918605e-012;

a₁ = -0.2135; a₇ = -3.70390824e-013.

a₂ = 0.1228;

a₃ = -0.0388;

a₄ = 0.00000189;

a₅ = 0.000000293;

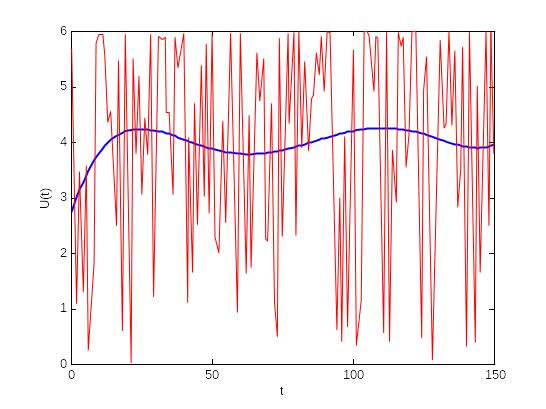
Рис. 2.2. Модель вхідного сигналу W(t), побудована поліномом Чебишева

2.4 Побудова моделі за допомогою перетворення Фур’є

Побудова моделі за допомогою перетворень Фур’є виконуємо тим же способом як і для вхідного сигналу U(t), що описаний в другому розділі.

Нижче наведено лістинг програмного модуля в середовищі Matlab:

clear;

load data.mat;

n=129;

Fur_por=4;

m=Fur_por;

for k=1:m+1

A=(1/n)*sum(n2wt);

B(k)=(2/n)*sum(n2wt.*cos(k*n2t));

C(k)=(2/n)*sum(n2wt.*sin(k*n2t));

end

for k=1:m+1

for i=1:n

FS(i,1)=A+sum(B(k)*sin(k*n2t(i))+C(k)*cos(k*n2t(i)));

end

end

plot(n2t,n2wt,'red')

hold on;

hPlot=plot(n2t,FS);

xlabel('t')

ylabel('W(t)')

axis([0,150,-0.5,6.5]);

set( hPlot, 'LineWidth', 2 );

Побудована модель представлена нижче, на рис. 2.3.

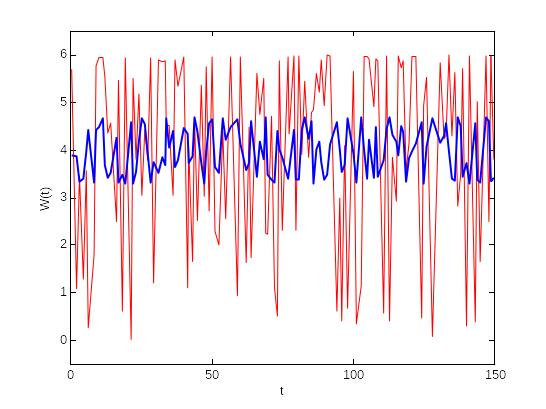
Рис. 2.3 - Модель вхідного сигналу W(t), побудована за допомогою перетворення Фур’є

Розв’язавши систему, отримаємо такі значення коефіцієнтів:

a₀ = 3.9924;