4.3 Побудова третьої моделі системи, виду

Y = a₀ +bcos(U(t)) + dsin(W(t))

За допомогою методу найменших квадратів знаходимо систему рівнянь, розв’язавши яку можна отримати коефіцієнти а₀, а₁, та а₂. За допомогою знайдених коефіцієнтів можна побудувати третю модель.

Система рівнянь буде мати вигляд:

Нижче приведемо лістинг модуля рішення даної системи:

clear;

load data.mat

for i=1:8;

for j=1:8;

A(i,j)=sum(n1t.^(i+j-2));

end;

end;

for i=1:8;

B(i)=sum(n1t.^(i-1).*n1ut);

end;

a1=B/A;

t=1:150;

f1=a1(8)*t.^7+a1(7)*t.^6+a1(6)*t.^5+a1(5)*t.^4+a1(4)*t.^3+a1(3)*t.^2+a1(2)*t+a1(1);

for i=1:8;

for j=1:8;

A(i,j)=sum(n2t.^(i+j-2));

end;

end;

for i=1:8;

B(i)=sum(n2t.^(i-1).*n2wt);

end;

a2=B/A;

f2=a2(8)*t.^7+a2(7)*t.^6+a2(6)*t.^5+a2(5)*t.^4+a2(4)*t.^3+a2(3)*t.^2+a2(2)*t+a2(1);

for i=1:8;

for j=1:8;

A(i,j)=sum(n3t.^(i+j-2));

end;

end;

for i=1:8;

B(i)=sum(n3t.^(i-1).*n3yt);

end;

a3=B/A;

f3=a3(8)*t.^7+a3(7)*t.^6+a3(6)*t.^5+a3(5)*t.^4+a3(4)*t.^3+a3(3)*t.^2+a3(2)*t+a3(1);

n=150;

Fur_por=3;

m=Fur_por;

for k=1:m+1

Am=(1/n)*sum(f3);

Bm(k)=(2/n)*sum(f3.*cos(k*f1));

Cm(k)=(2/n)*sum(f3.*sin(k*f2));

end

for k=1:m+1

for i=1:n

sysmod3(i)=Am+sum(Bm(k)*sin(k*f1(i))+Cm(k)*cos(k*f2(i)));

end

end

hPlot=plot(t,f3,'red');

hold on;

hPlot1=plot(t,sysmod3);

grid on;

xlabel('t')

ylabel('Y(t)')

set( hPlot,'LineWidth', 2 );

set( hPlot1,'LineWidth', 2 );

S3=sqrt((sum(f3-sysmod3)^2)/(n-2));

Розв’язавши її, знайдемо коефіцієнти а, b, c, які визначатимуть модель:

a₀ = 2.3812;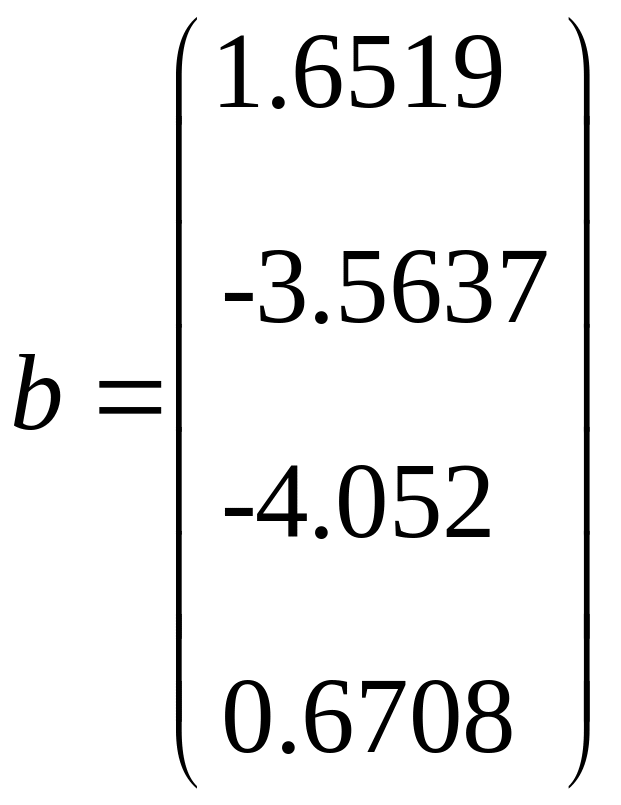

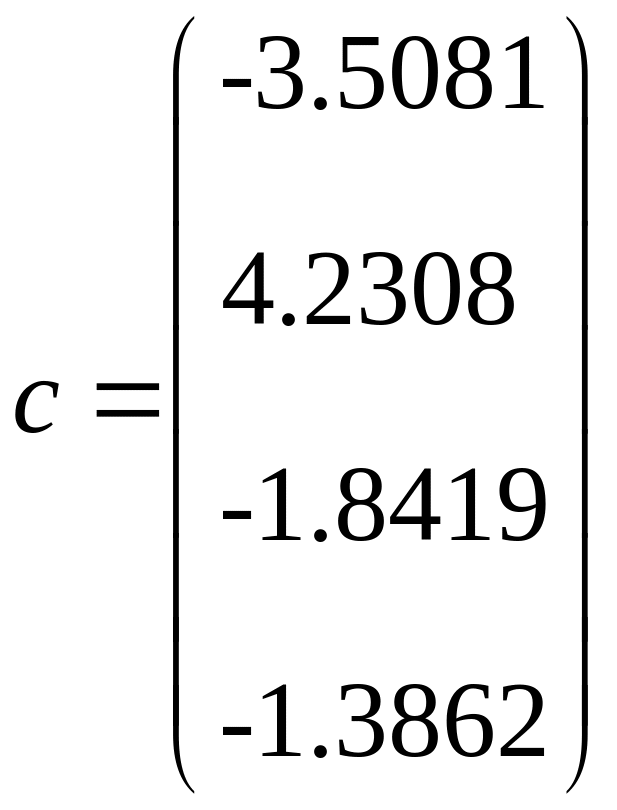
Нижче побудуємо графічне представлення моделі, на якому видно її співвідношення до реального об’єкта.

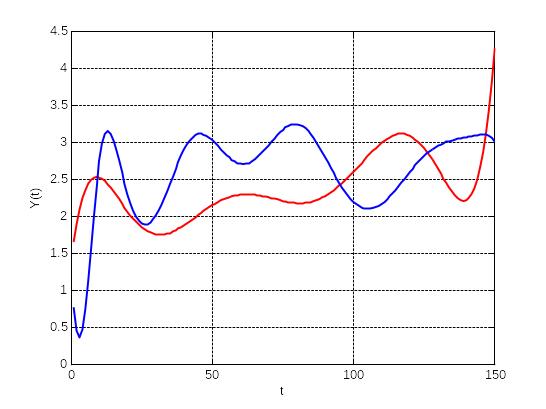
Рис. 4.3 – Загальна модель системи виду

Y = a₀ +bcos(U(t)) + dsin(W(t))

4.4 Вибір оптимальної моделі

Вибір оптимальної моделі системи будемо здійснювати за тим самим критерієм, що й вибір оптимальних моделей для функцій U(t), W(t), Y(t).

Приведемо лістинг розрахунку:

S1=sqrt((sum(f3-sysmod1)^2)/(n-2));

S2=sqrt((sum(f3-sysmod2)^2)/(n-2));

S3=sqrt((sum(f3-sysmod3)^2)/(n-2));

Значення результатів розрахунків по критерію для моделей зведемо в таблицю:

Оптимальні значення моделей

Таблиця 4.1

Номер можелі	S1	S2	S3
Значення критерію	8.3959e-016	5.7935	2.9667

Отже, оптимальною моделлю є модель, що описується рівнянням виду:

Y = a₀+a₁ U(t)+a₂W(t)

Висновок

Математична модель є наближеним описом будь-якого класу явищ зовнішнього світу, вираженим за допомогою математичної символіки. Математична модель - могутній метод пізнання зовнішнього світу, а також прогнозування і управління. Аналіз математичної моделі дозволяє проникнути в суть явищ, що вивчаються.

Метод математичного моделювання, що зводить дослідження явищ зовнішнього світу до математичних задач, займає ведуче місце серед інших методів дослідження, особливо в зв'язку з появою ЕОМ. Він дозволяє проектувати нові технічні засоби, працюючі в оптимальних режимах, для рішення складних задач науки і техніки; проектувати нові явища. Математичні моделі виявили себе як важливий засіб управління. Вони застосовуються в самих різних областях знання, стали необхідним апаратом в області економічного планування і є важливим елементом автоматизованих систем управління.

За допомогою використання математичного моделювання ми визначили можливості опису випадкових процесів математичними моделями різних видів. З чого було видно, що різні характеристики одного й того ж випадкового процесу мають різні адекватні моделі. Тому слід відмітити, що для опису характеристик випадкового процесу, для адекватності оцінки об’єкта чи система потрібно будувати декілька математичних моделей, з яких вибирати найбільш оптимальну. Але все рівно, складність об’єктів буває настільки великою, що навіть опис складними рівняннями не дасть повної відповідності та точності щодо реального об’єкта.