Оптимизация показателей надежности

Поскольку материальные затраты на изготовление различных элементов какой-либо системы неодинаковы, то оказывается, что при ограничении материальных средств максимальной надежности системы можно достичь, используя неравно надежные элементы.

Действительно, можно существенно повысить надежность системы из последовательно (в функциональном смысле) созданных элементов, если незначительно снизить затраты на изготовление сложного, то есть дорогостоящего, элемента и употребить освобожденные средства на повышение надежности менее дорогого, то есть простого, элемента.

Налицо оптимизационная задача достижения максимально возможного уровня надежности при наличии ограничений. Для решения таких задач успешно используется метод динамического программирования. С целью уяснения сущности этого метода рассмотрим задачу о минимизации функции.

Задача о минимизации функции

Имеем функцию

F(x₁, x₂, x₃)=a₁x₁² + a₁x₂² + a₁x₃² (4.18)

При этом х₁+х₂+х₃=с; х₁≥0, х₂≥0, х₃≥0. (4.19)

а₁+а₂+а₃ – известные положительные величины.

Допустим, что С – ресурсы, которые надо распределить таким образом, чтобы функция (4.18) была минимальной. Иными словами, надо найти

Х_i=f_i(c, a₁, a₂, a₃); i=1, 2, 3, чтобы F=F_мин.

Решение.

1. Введем дополнительные обозначения:

х₁=с₁; х₁+х₂=с₂; х₁+х₂+х₃=с₃ (4.20)

2. Разделим ресурсы с на две части: х₃ и с — х₃ = с₂

запишем так называемое рекуррентное соотношение:

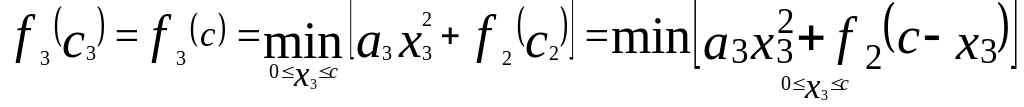(4.21)

которое можно трактовать таким образом: найти такую функцию от С, которая в пределах 0 ≤ х₃ ≤ С достигала бы минимума при выделении части х₃ ресурсов для третьей составляющей функции F и части (с  х₃) ресурсов для оставшихся двух составляющих.

Примечание. В математике рекуррентной формулой называют формулу, выражающую каждый член последовательности через предыдущие члены. Здесь с₂=сх₃ сумма предыдущих членов.

3. Разделим оставшуюся после выделения х₃ часть ресурса с₂ = с—х₃ на две части: х₂ и (с₂ х₂).

Тогда функция, достигающая минимума в пределах 0≤х₂≤с₂ имеет выражение

(4.22)

4. Оставшаяся часть ресурсов — это ресурсы, приходящиеся на первую составляющую:

f₁(c₁)=f₁(x₁)=f₁(c₂x₂)=a₁c₁²=a₁(c₂x₂)². (4.23)

теперь эти формулы - (4.21), (4.22), (4.23) - путем подстановок надо «пройти» дважды: снизу вверх (от конца к началу), подставляя последующие формулы в предыдущие, при этом находят условно оптимальные значения х_i1, выраженные через с_i , и сверху вниз (от начала к концу) — при этом определяются строго оптимальные значения х_iопт =f_i (с, а₁, а₂, а₃).

5. Подставим (4.23) в (4.22) и найдем х₂ =f₂(с₂, a₁, а₂), минимизирующее функциюf₂ (с₂). Имеем

f₂(c₂)=min [a₂x₂²+a₁(c₂x₂)²] (4.24)

^0≤x₂^{≤ C}₂

Берем производную от выражения в квадратных скобках и приравняем ее к нулю:

[a₂x₂²+a₁(c₂+x₂)²]' =2a₂x₂2a₁c₂+2a₁x₂=0.

Тогда

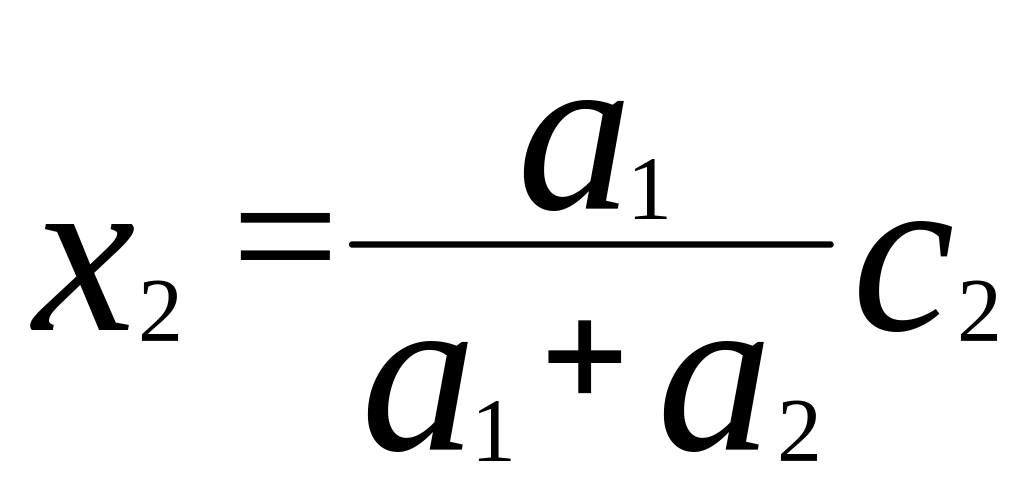. (4.25)

(Поскольку вторая производная, 2(а₁+а₂), положительна, значение (4.25) сообщает функции (4.24) минимум).

Подставляя (4.25) в (4.24), получаем

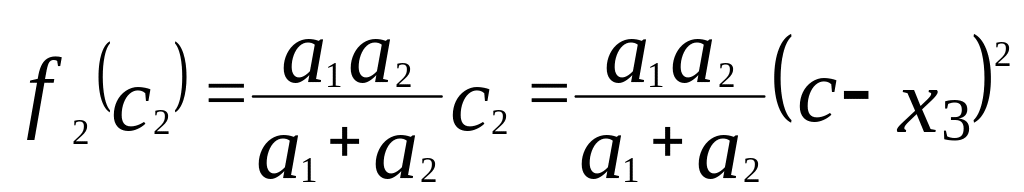. (4.26)

После подстановки (4.26) в (4.21) возьмем производную по х₃ от выражения в квадратных скобках и. приравнивая ее к нулю, определим оптимальное (уже не условное) значение х_{3 опт}:

;

;

.

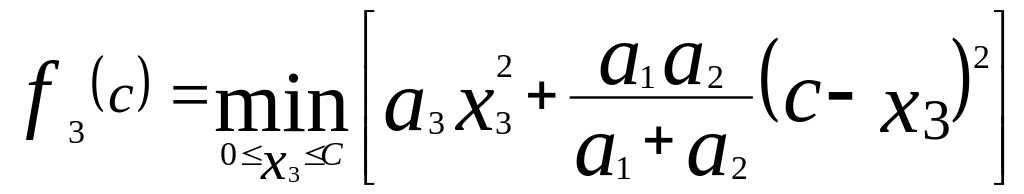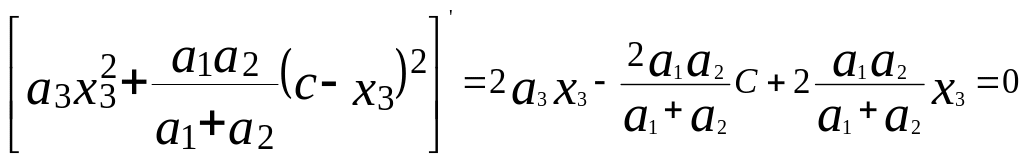Подставим в (4.25) вместо С₂ значение С₂=СХ_{3 опт} тогда

(4.27)

Наконец, определим, Х_{1 опт}=С₁=С₂Х_{2 опт}=СХ_{3 опт}Х_{2 опт}

(4.28)