2. Кореляційний момент і коефіцієнт кореляції.

Для характеристики кореляційної залежності між величинами використовуються кореляційний момент і коефіцієнт кореляції.

В и з н а ч е н н я 2. Кореляційним моментом µ_xy випадкових величин X і Y називають математичне сподівання похідної відхилень цих величин

Для обчислення кореляційного моменту дискретних величин використовується вираз

(3.12)

а для неперервних – вираз

(3.13)

З а у в а ж е н н я. Кореляційний момент µ_xy може бути переписаний у вигляді

(3.14)

Дійсно, використовуючи властивості математичного сподівання (див. §§ 2.2; 2.6), маємо

Т е о р е м а. Кореляційний момент двох незалежних випадкових величин X і Y дорівнює нулю.

Д о в е д е н н я. Згідно зауваження

а оскільки Х і Y незалежні випадкові величини, то (див. §§ 2.2; 2.6)

а, отже µ_xy=0.

З визначення кореляційного моменту виходить, що він має розмірність, яка дорівнює похідній величин X і Y, тобто його величина залежить від одиниць вимірювання випадкових величин. Тому для одних і тих же двох величин величина кореляційного моменту може мати різні значення залежно від того, в яких одиницях були виміряні величини. Для усунення цього недоліку домовилися за міру зв'язку (залежності) двох випадкових величин X і Y прийняти безрозмірну величину

(3.15)

де σ_х=σ(Х), σ_y=σ(Y), яка називається коефіцієнтом кореляції.

П р и к л а д 1. Нехай двовимірна дискретна випадкова величина (X,Y) задана законом розподілу:

x\y	1	2	3
1	1\18	1\12	1\36
2	1\9	1\6	1\18
3	1\6	1\4	1\12

Знайдемо кореляційний момент і коефіцієнт кореляції випадкових величин X і Y.

Розв’язок. Додавши імовірності по рядкам, отримаємо імовірності можливих значень X:

Звідси закон розподілу X:

X	1	2	3
p	1\6	1\3	1\2

а, отже

Додавши ж імовірності по стовпцях, знайдемо імовірності можливих значень Y:

Звідси закон розподілу Y:

Y	1	2	3
p	1\3	1\2	1\6

і, отже

Отже

Таким чином, коефіцієнт кореляції

Т е о р е м а. Абсолютна величина кореляційного моменту двох випадкових величин не перевершує похідної їх середніх квадратичних відхилень:

Д о в е д е н н я. Ввівши в розгляд випадкову величину де знайдемо її дисперсію. Маємо

(будь-яка дисперсія ненегативна). Звідси

Ввівши випадкову величину , аналогічно знайдемо

В результаті маємо

або

(3.16)

В и з н а ч е н н я 2. Випадкові величини X і Y називаються некорельованими, якщо = 0, і корельованими, якщо

П р и к л а д 1. Незалежні випадкові величини Х і Y є некорельованими, оскільки через співвідношення (3.12) = 0.

П р и к л а д 2. Нехай випадкові величини Х і Y зв'язані лінійною залежністю Знайдемо коефіцієнт кореляції. Маємо:

звідки

Тому

Таким чином, коефіцієнт кореляції випадкових величин, зв'язаних лінійною залежністю, рівний ±1 (точніше =1, якщо А>0 і =-1, якщо А<0).

Відзначимо деякі властивості коефіцієнта кореляції.

З прикладу 1 слідує:

1) Якщо X і Y — незалежні випадкові величини, то коефіцієнт кореляції рівний нулю.

Відмітимо, що зворотне твердження, взагалі кажучи, невірне. (Доказ див. в роботі [2].)

2)Абсолютна величина коефіцієнта кореляції не перевершує одиниці:

Дійсно, розділивши обидві частини нерівності (3.16) на похідну , приходимо до шуканої нерівності.

3) Як видно з формули (3.15) з урахуванням формули (3.14), коефіцієнт кореляції характеризує відносну величину відхилення математичного сподівання похідної від похідних математичних сподівань М(Х) М(Y) величин X і Y. Оскільки це відхилення має місце тільки для залежних величин, то можна сказати, що коефіцієнт кореляції характеризує тісноту залежності між X і Y.

3. Лінійна кореляція. Цей вид кореляційної залежності зустрічається досить часто.

В и з н а ч е н н я. Кореляційна залежність між випадковими величинами Х і Y називається лінійною кореляцією, якщо обидві функції регресії і є лінійними. В цьому випадку обидві лінії регресії є прямими; їх називають прямими регресії.

Виведемо рівняння прямої регресії Y на X, тобто знайдемо коефіцієнт лінійної функції

Позначимо М(Х)= а, М(Y) = b, М[(Х - а)²] = , М[(Y –b²)] = . З використанням властивостей МО (§§ 2.2; 2.6) знаходимо:

М(Y)= М[g(Х)] = М(АХ + У)= АМ(Х)+ У

тобто b = Аа + У, звідки В=b-Аа.

Далі, за допомогою тих же властивостей математичного сподівання маємо

М(ХY) = М[Хg(Х)\ = М(АХ2 + ВХ) = АМ(Х2)+ ВМ(Х) = АМ(Х2)+ (b- Аа)а

звідки

А=

або, згідно властивості 1 дисперсії (§§ 2.3; 2.6)

Отриманий коефіцієнт називається коефіцієнтом регресії Y на X і позначається через :

(3.17)

Таким чином, рівняння прямої регресії Y на X має вигляд

(3.18)

Аналогічно можна отримати рівняння прямої регресії X на Y

(3.19)

де

(3.20)

коефіцієнт регресії X на Y.

Рівняння прямих регресії можна записати в більш симетричному вигляді, якщо скористатися коефіцієнтом кореляції. З урахуванням цього коефіцієнта маємо:

(3.21)

і тому рівняння прямих регресії приймають вигляд:

З рівнянь прямих регресії видно, що обидві ці прямі проходять через точку (а;b); кутові коефіцієнти прямих регресії рівні відповідно (мал. 13):

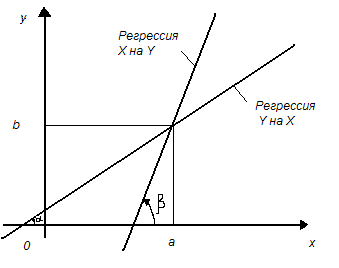
мал. 13

Оскільки те Це означає, що пряма регресії Y на X має менший нахил до осі абсцис, чим пряма регресії X на Y. Чим ближче до одиниці, тим менше кут між прямими регресії. Ці прямі зливаються тоді і тільки тоді, коли =1.

При = 0 прямі регресії описуються рівнянням у=b; х = а.

В цьому випадку МХ(Y)= b = М(Y); МУ(Х)= а = М(Х).

З формули (3.21) видно, що коефіцієнти регресії мають той же знак, що і коефіцієнт кореляції , і зв'язані співвідношенням