§ 3.6. Незалежність випадкових величин

Т е о р е м а. Для того, щоб випадкові величини X і Y були незалежними, необхідно і достатньо, щоб функція розподілу системи (X,Y) дорівнювала похідній функції її складових:

F(x,y)=F₁(x)F₂(y).

Д о в е д е н н я.

Н е о б х і д н і с т ь. Нехай X і Y незалежні. Тоді події Х<х і Y<y незалежні, отже, імовірність поєднання цих подій рівна похідній їх імовірностей.

Р(Х<х, Y<y)=P(X<x)P(Y<y)

або

F(x,y)=F₁(x)F₂(y).

Д о с т а т н і с т ь. Нехай F(x,y)=F₁(x)F₂(y). Звідси слідує, що імовірність поєднання подій Х<х і Y<y рівна похідній імовірності цих подій. Отже, величини X і Y незалежні.

Н а с л і д о к. Для того, щоб неперервні випадкові величини X і Y були незалежними, необхідно і достатньо, щоб щільність імовірності системи (X,Y) дорівнювала похідній щільності імовірності складових X і Y:

f(x,y)=f₁(x)f₂(y).

П р и к л а д. Двовимірна неперервна випадкова величина (X, Y) задана щільністю імовірності

Доведіть, що складові X і Y незалежні.

Розв’язок. Згідно з формулою (3.8)

Аналогічно згідно з формулою (3.8')

а, отже

f(x,y)=f₁(x)f₂(y)

тобто випадкові величини X і Y незалежні.

§ 3.7. Елементи теорії кореляції

1. Кореляційна залежність. Часто доводиться мати справу з складнішою залежністю, ніж функціональна. Такий, наприклад, зв'язок між опадами і урожаєм або зв'язок між товщиною снігового покриву взимку і об'ємом стоку подальшої повені. Тут кожному значенню однієї величини відповідає безліч можливих значень іншої величини. Подібного роду залежності відносяться до кореляційних залежностей.

В и з н а ч е н н я 1. Дві випадкові величини X і Y знаходяться в кореляційній залежності, якщо кожному значенню будь-якої з цих величин відповідає певний розподіл імовірності іншої величини.

В и з н а ч е н н я 2. Умовним математичним сподіванням дискретної випадкової величини X при Y=y (у – певне можливе значення Y) називається сума похідних можливих значень величини X на їх умовні імовірності:

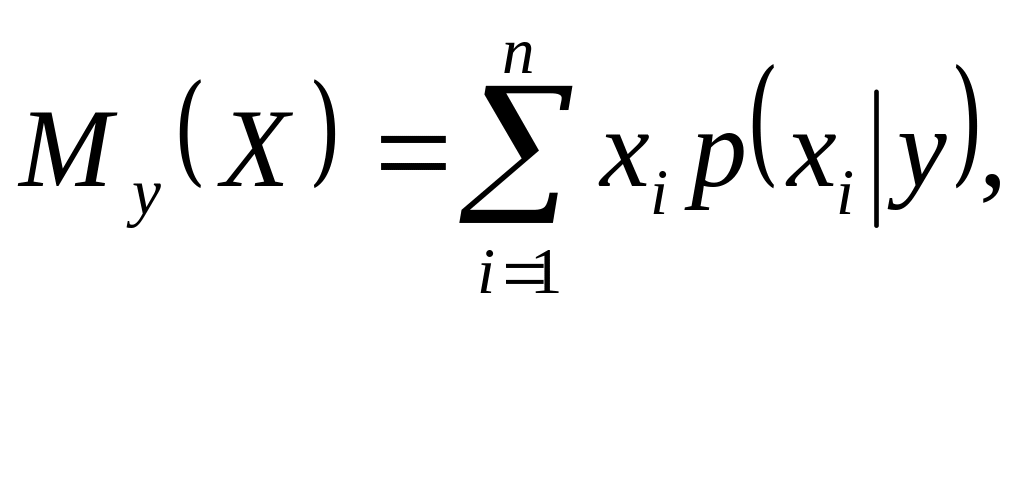
де р(х_i|у) – умовна імовірність рівності Х=х_i за умови, що Y=y.

Для неперервних величин

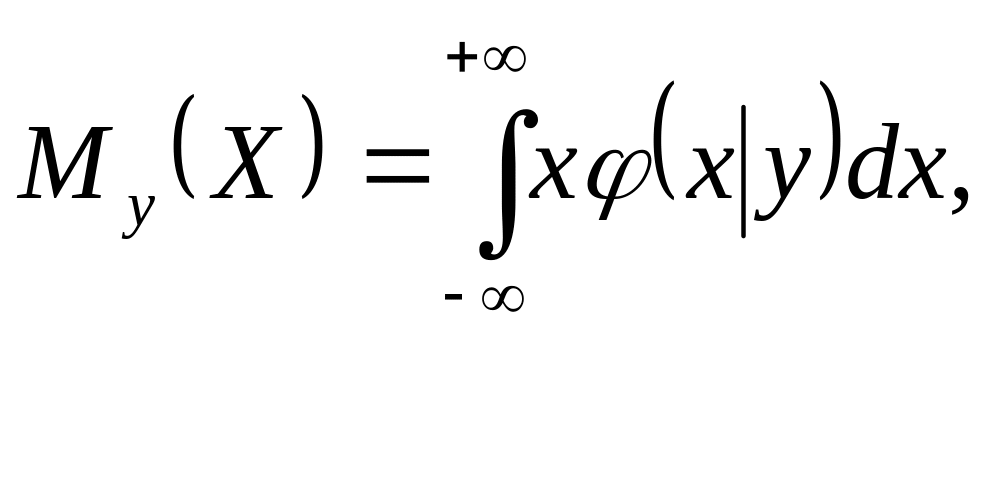
де (х|у) – щільність імовірності випадкової неперервної величини X за умови Y=y.

Умовне математичне сподівання М_у(Х) є функція від у: M_y(X)=f(y), яку називають функцією регресії величини X на величину Y.

Аналогічно визначаються умовне математичне сподівання випадкової величини Y і функція регресії Y на X:

Рівняння x=f(y) (y=g(x)) називається рівнянням регресії X на Y (Y на X), а лінія на площині, відповідна цьому рівнянню, називається лінією регресії.

Лінія регресії Y на X (X на Y) показує, як в середньому залежить Y від X (X від У).

П р и к л а д 1. Хай Х і Y незалежні; М(Х)=а, М(Y)=b. Тоді g(x)=М_х(Y)₌M(Y)=b; f(y)=М_y(Х)=М(Х)=а_. Лінії регресії зображені на мал. 12.

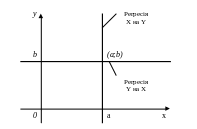
Мал. 12

П р и к л а д 2. Х і Y зв'язані лінійною залежністю: Y=AX+B, А≠0. Тоді функція регресії Y на X матиме вигляд

g(x)=M_x(Y)=М(Ах+В)=Ах+В.

Оскільки , то функція регресії X на Y має вигляд

Значить, лінія регресії X на Y: х= (у-В)/А, тобто у=Ах+В. Таким чином, у разі лінійної залежності X і Y лінії регресії X на Y і Y на X співпадають, і ця лінія пряма.