§ 3.5. Умовні закони розподілу складових двовимірних дискретних і неперервних випадкових величин

1. Умовні закони розподілу складових двовимірних дискретних випадкових величин.

Розглянемо дискретну двовимірну випадкову величину (X, Y). Нехай можливі значення складових х_1, х₂, ..., х_n; у_1, у_2, ...,у_m.

Припустимо, що в результаті випробування величина Y прийняла значення Y=y₁; при цьому X прийме одне із своїх можливих значень: x₁ або x₂ ..., або х_n. Позначимо умовну імовірність того, що X прийме, наприклад, значення х₁ за умови, що Y=y₁ через p(x₁|y₁). У загальному випадку умовну ймовірність складової позначатимемо так:

В и з н а ч е н н я. Умовним розподілом складової X при У=у₁ називають сукупність умовної імовірності

^

обчислених в припущенні, що подія Y=y₁ вже настала.

Так само визначаються і умовні розподіли X при Y=y₂, У=у₃ ..., Y=y_m.

Аналогічно визначаються умовні розподіли складової Y.

Знаючи закон розподілу двовимірної дискретної випадкової величини, можна, скориставшись формулою

(див. § 1.3, п. 2, формула (1.7)),

отримати умовні закони розподілу складових. Так, умовний закон розподілу Х в припущенні, що подія Y=y₁ вже відбулася, може бути знайдений за формулою

(3.9)

Аналогічно знаходять умовні закони розподілу складової Y. Наприклад, умовний закон розподілу У в припущенні, що подія Х=x₂ вже відбулася, є

З а у в а ж е н н я. Сума імовірності умовного розподілу дорівнює одиниці. Дійсно, наприклад,

Цю властивість використовують для контролю обчислень.

П р и к л а д. Дискретна двовимірна випадкова величина задана таблицею

x\y	y1	y2
x1	0,10	0,06
x2	0,30	0,18
x3	0,20	0,16

Знайдемо умовний закон розподілу складової X за умови, що складова Y прийняла значення y₁.

Розв’язок. Шуканий закон визначається сукупністю умовної імовірності:

Скориставшись формулою (3.9) і прийнявши до уваги дані вказаної таблиці (р(х₁,y₁₎=0,10, р(х₂,у₁₎=0,30, р(х₃,у₁₎=0,20) і що р(у₁)=0,60 (§ 3.1, приклад), маємо:

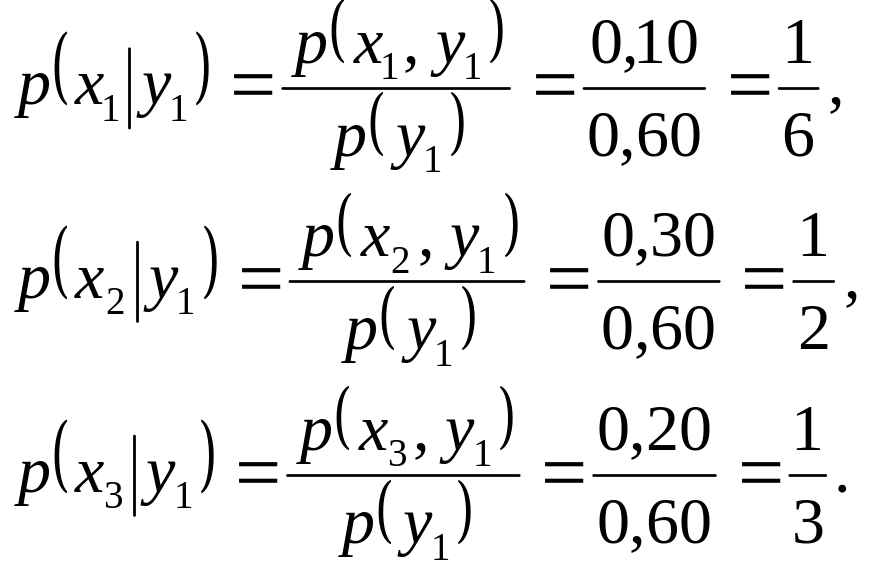
2. Умовні закони розподілу складових двовимірних неперервних випадкових величин.

Нехай (X,Y) – неперервна двовимірна випадкова величина.

В и з н а ч е н н я. Умовною щільністю (х|у) розподілу складової X при даному значенні Y=y називають відношення двовимірної щільності імовірності f(х,у) до щільності ймовірності f₂(у) складової Y:

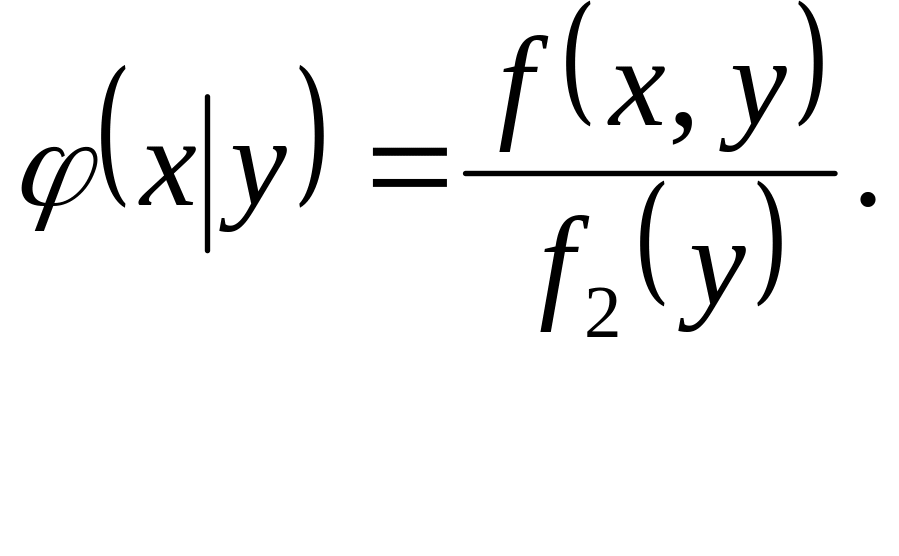(3.10)

Відмінність умовної щільності (х|у) від щільності f₁(х) складової X полягає в тому, що функція (х|у) дає розподіл X за умови, що складова Y прийняла значення Y=y; функція ж f₁(х) дає розподіл X незалежно від того, які з можливих значень прийняла складова Y.

Аналогічно визначається умовна щільність складової Y при даному значенні Х=х:

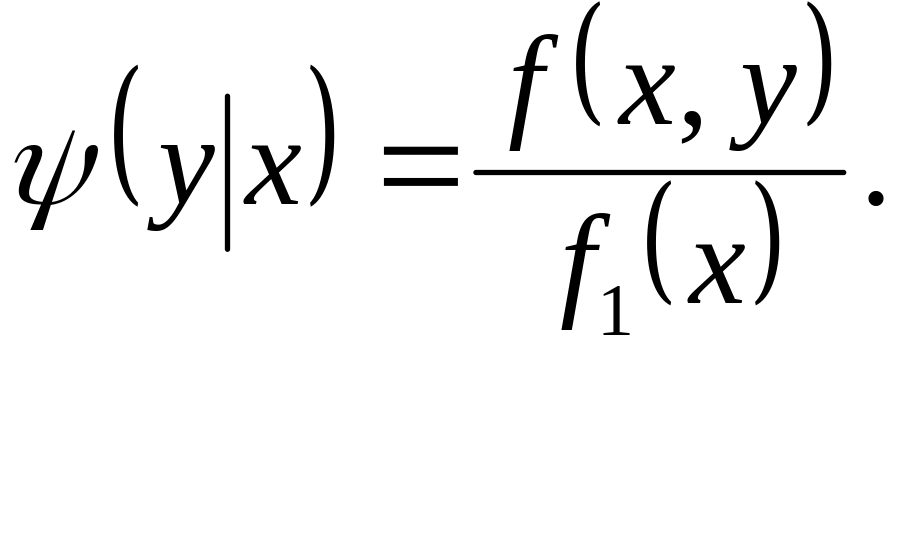(3.11)

Формули (3.10) і (3.11) з урахуванням формул (3.8') і (3.8) можуть бути переписані і в наступному вигляді:

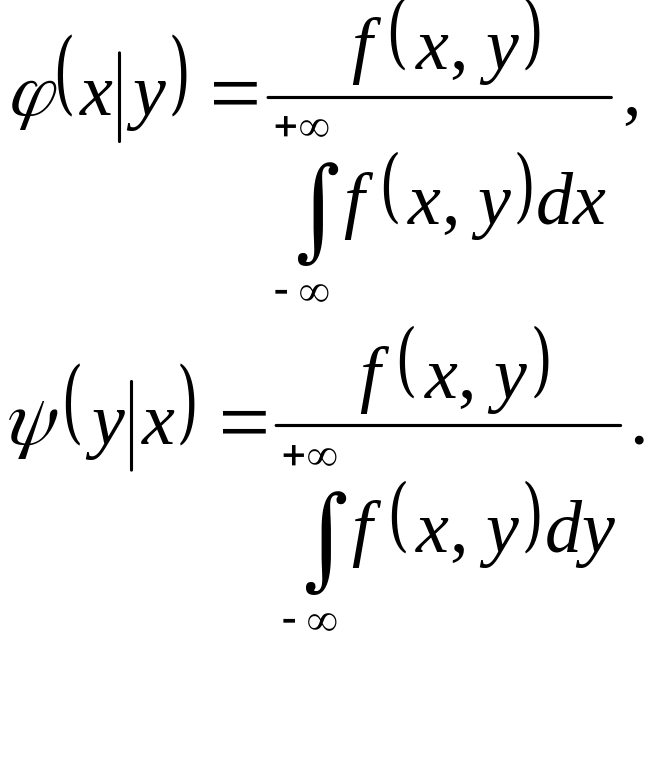
Зазначимо, що, як і будь-яка щільність, умовні щільності мають властивості:

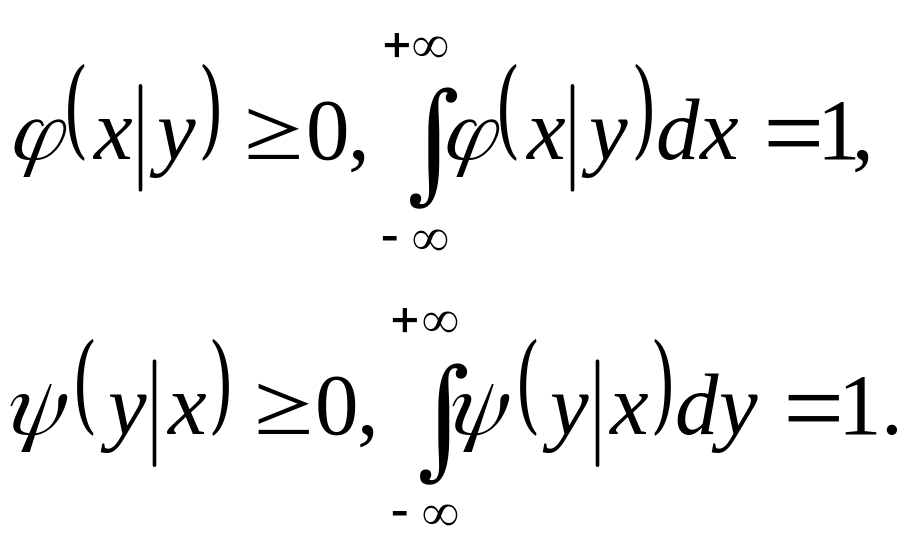
П р и к л а д. Нехай двовимірна випадкова величина (X,Y) задана щільністю імовірності

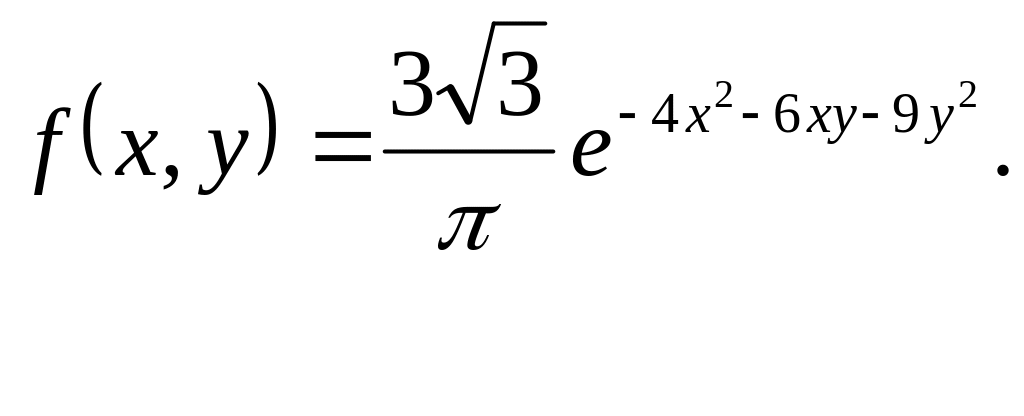
Потрібно знайти умовну щільність імовірності складових X і Y.

Розв’язок. Раніше (див. § 3.4, приклад) була знайдена щільність імовірності складових X і Y

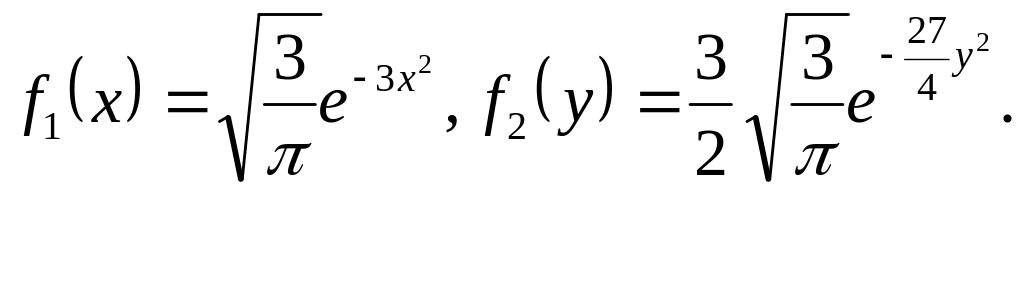
Тому, згідно формул (3.10) і (3.11), знайдемо:

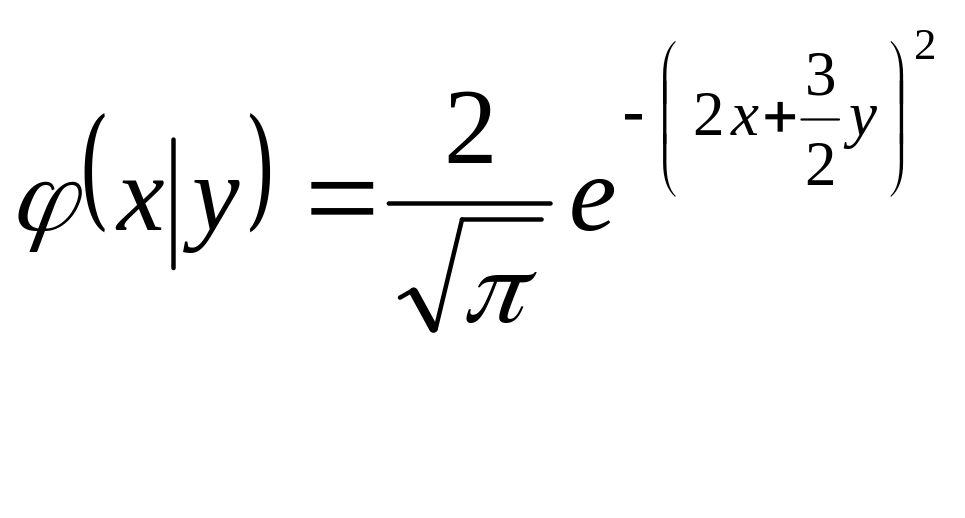
і