§ 3.2. Функція розподілу двовимірної випадкової величини

1. Визначення функції розподілу двовимірної випадкової величини і її властивості.

В и з н а ч е н н я. Функцією розподілу двовимірної випадкової величини (X, У) (байдуже, дискретної або безперервної) називають функцію F(x, у), що визначає для кожної пари дійсних чисел x, у ймовірність того, що X прийме значення, менше x, і при цьому У прийме значення, менше у:

F(x, у)= P(X< x, Y< у).

y

A(x; y) Геометрично (мал.9) ця рівність являє

собою ймовірність того, що випадкова

точка (X, Y) потрапить в безкінечний квадрант з вершиною (x, y), яка 0 x розташована лівіше і нижче цієї вершини. П р и к л а д. Знайдіть ймовірність того, що в результаті випробування складова X

двовимірної випадкової величини (X, Y)

Мал. 9 набуде значення X<4 і при цьому складова Y набуде значення Y<5, якщо відома функція розподілу цієї величини.

Р о з в ’ я зок. Маємо

.

Вкажемо властивості, якими володіє функція F (x, у).

1. 0 ≤ F (x, у) ≤ 1.

Ця властивість виходить з того, що F (x, у) ймовірність.

2. F (x, у) – неспадна по кожному аргументу, тобто

F (x₁, у) ≤ F (x₂, у), якщо x₁ < x₂;

F (x, y₁) ≤ F (x, y₂), якщо y₁ < y₂.

Властивість стає наочною, якщо скористатися геометричною інтерпретацією функції розподілу.

3. Мають місце граничні співвідношення:

,

.

Ці співвідношення також виходять з геометричної інтерпретації функції розподілу.

4. При 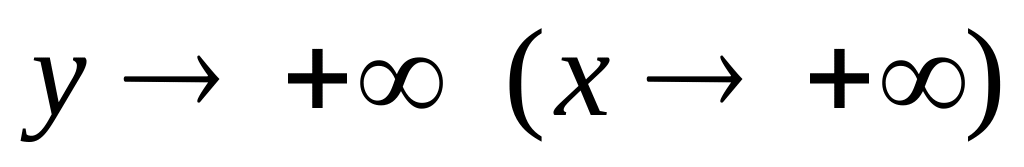функція розподілу системи прямує до функції розподілу, яка становить X(Y):

;

.

Дійсно, при безкінечний квадрант з вершиною в точці А(x, у) перетворюється на напівплощину, ймовірність попадання в яку є функція розподілу, яка становить X(Y).

2. Ймовірність попадання випадкової точки в напівсмугу і прямокутник.

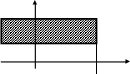
1. Знайдемо ймовірність того, що в результаті випробування випадкова точка потрапить в напівсмугу x₁ < X < x₂ і y₁ < У < y₂ (мал. 10, б).

Віднімаючи від ймовірності попадання випадкової точки в квадрант з вершиною (x₂; y₁) ймовірність попадання цієї точки в квадрант з вершиною (x₁; y₁) (мал. 10, а) отримаємо

P(x1 ≤ X < x₂, У < y₁)= F(x₂, y₁) – F(x₁, y₁).

Аналогічно

P(X < x₁, y₁ ≤ У < y₂)= F(x₁, y₂) – F(x₁, y₁).

у у

(x₁, y₁) (x₂, y₁)

y₁

0 x₁ x₂ x 0 x₁ x

а б

Мал. 10

Отже, ймовірність попадання випадкової точки в напівсмугу дорівнює приросту функції розподілу по одному з аргументів.

2. Знайдемо ймовірність попадання випадкової точки (X; У) в прямокутник ABCD (мал. 11).

у А(x₁, y₂) B(x₂, y₂)

y₁ D (x₁; y₁) С(x₂; y₁)

0 x₁ x₂ x

Мал. 11

Для цього від ймовірності попадання випадкової точки в напівсмугу AB з вертикальним штрихуванням віднімемо ймовірність попадання цієї точки в напівсмугу DC з горизонтальним штрихуванням. Отримаємо

P(x₁ ≤ X < x₂, y₁ ≤ У < y₂)=

= (F(x₂, y₂) – F(x₁, y₂)) – (F(x₂, y₁) – F (x₁, y₁)). (3.1)

П р и к л а д. Знайдемо ймовірність попадання випадкової точки (X, У) в прямокутник, обмежений прямими, якщо відома функція розподілу

.

Розв’язок. В даному прикладі у виразі (3.1), і, означає

.