§ 2.9. Граничні теореми теорії ймовірності

1. Центральна гранична теорема. Як вже зазначалось, нормально розподілені випадкові величини досить розповсюджені на практиці. Пояснення цьому дає центральна гранична теорема, один із варіантів її формулювання належить російському математику А.М Ляпунову(1857-1918). Суть центральної граничної теореми полягає в наступному: якщо випадкова величина Х являє собою суму дуже великого числа незалежних випадкових величин, вплив кожної із яких на всю суму мізерно малий, то Х має розподіл, близький до нормального.

Наведемо без доведення (доведення дивитись в роботі [3]) центральну граничну теорему для випадку однаково розподілених випадкових величин.

Теорема. Якщо Х₁, Х₂ ..., Х_n – незалежні випадкові величини, котрі мають одне й те саме розподілення із математичним сподіванням α та дисперсією σ² , то при необмеженому збільшені n закон розподілення суми

Х=Х₁ + Х₂ +... + Х_n необмежено наближається до нормального.

2. Локальна та інтегральна граничні теореми Лапласа.

Якщо число випробувань n велике, то розрахунки по формулі Бернуллі стає робити більш проблематично. Лаплас отримав важливу наближену формулу для розрахунку ймовірності Р_n(m) появи події А точно m раз, якщо n – досить велике число. Ним же й отримана наближена формула і для суми виду .

Локальна гранична теорема Лапласа. Нехай р= Р(А) – ймовірність події А, при чому 0<p<1. Тоді ймовірність того, що в умовах схеми Бернуллі подія А при n випробувань появиться рівно m раз, виражається наближеною формулою

(2.39)

де q=1-p;

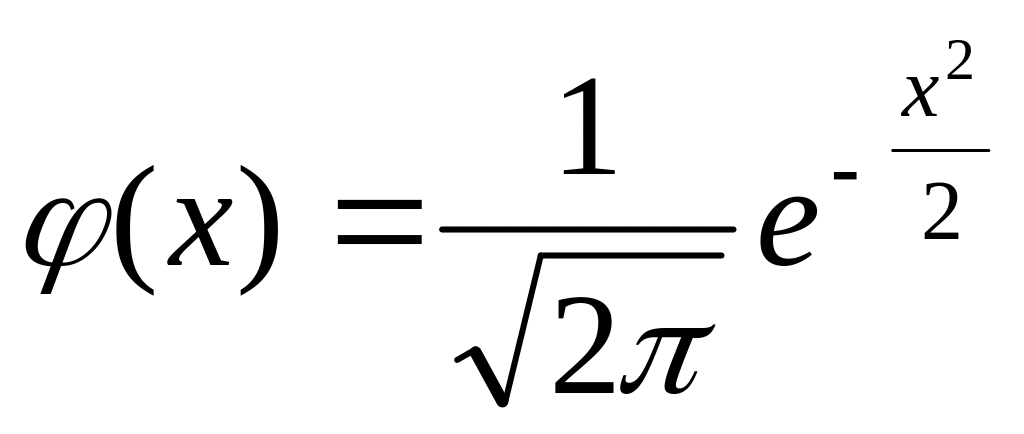
Для функції φ(х) складена таблиця(див. додаток 2) її значення для позитивних значень х [функція φ(х) парна].

Вираз (2.39) називають формулою Лапласа.

П риклад 1. Ймовірність попадання в ціль мисливця при одиничному пострілі p= 0,2. Яка ймовірність того, що при 100 пострілах ціль буде уражена рівно 20 раз?

З відси p = 0,2, q=0,8, n=100 та m = 20. Звідси і, отже,

Враховуючи, що φ (0) = 1/ = 0,40, з формули (2.39) отримуємо

Перейдемо до інтегральної теореми Лапласа. Поставимо наступне питання: яка ймовірність того, що в умовах схеми Бернуллі подія А, котра має ймовірність Р(А) =р(0<р< 1) при n випробуваннях (як і раніше число випробувань велике), з'явиться не менше k і не більше l разу? Цю шукану ймовірність позначимо Рn(k,l).

На основі теореми додавання ймовірностей для несумісних подій (§ 1.3, п. 1) отримаємо

(2.40)

де

(2.41)

Далі в силу рівності (2.41) маємо

(2.42)

і тому

Т ут сума справа являється інтегральною сумою для функції φ(х) на відрізку , причому, як слідує із нерівності (2.42), при

Отже, при n→∞ границя вказаної інтегральної суми є визначеним інтегралом

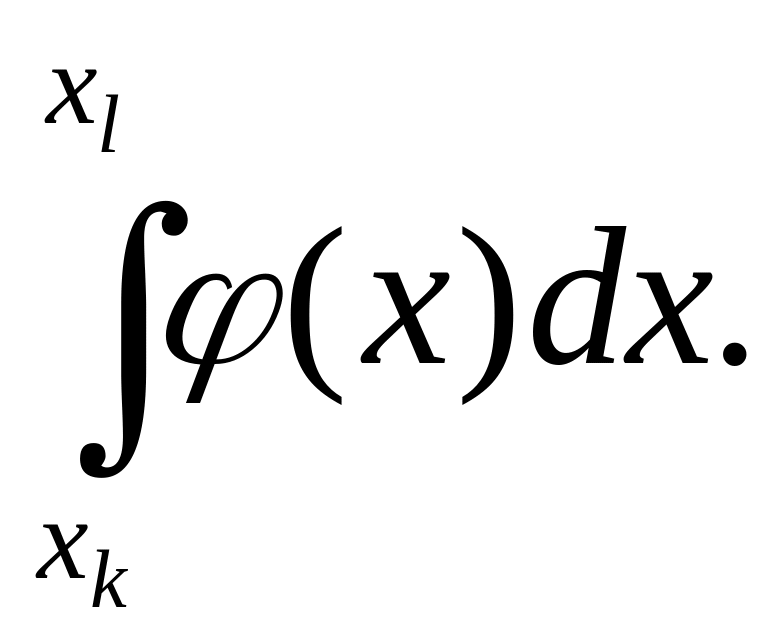
Т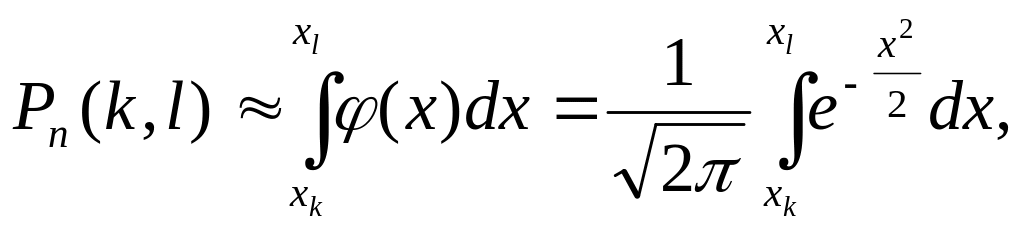 ому

(2.43)

д е

(2.44)

В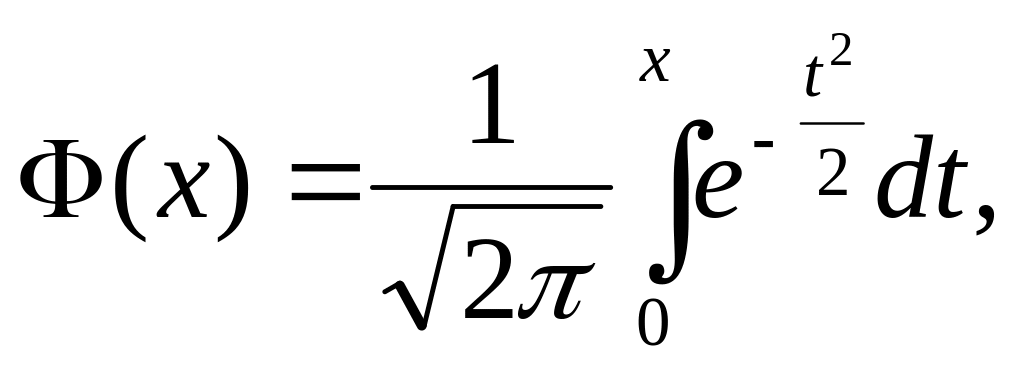 ираз (2.43) при умові (2.44) і складає зміст інтегрально граничної теореми Лапласа. Нами вже було доведена функція

(2.45)

котра називається функцією Лапласа, або інтегралом ймовірності. Очевидно, Ф(х) є первісною для функції φ(х). Тому на основі формули Ньютона – Лейбніца із формули (2.43) отримаємо

(2.46)

(інтегральна формула Лапласа).

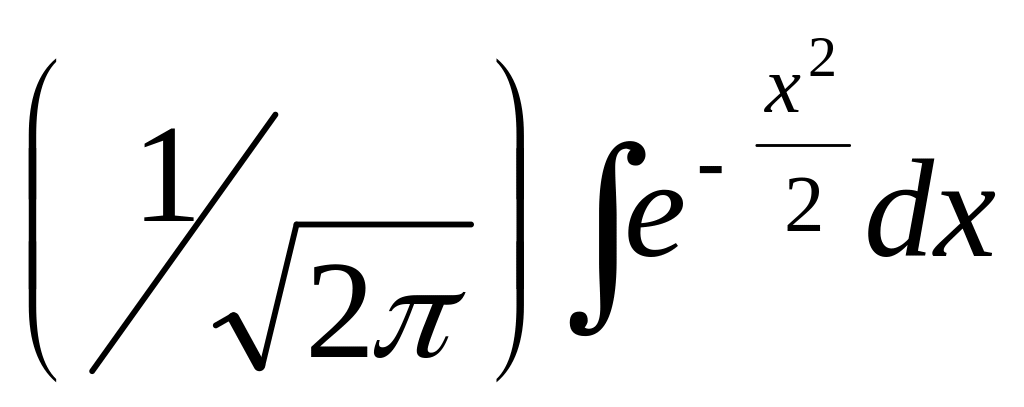
Як відомо, інтеграл не береться в елементарних функціях. Тому для функції (2.45) створена таблиця (див. додаток 3) її значень для додатних значень х, так як Ф(0)=0 і функція Ф(х) непарна:

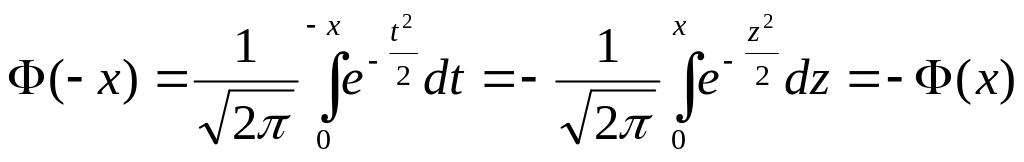
(t=-z, dt=-dz)

Приклад 2. Ймовірність того, що виріб пройшов перевірку р = 0,2. Знайдемо ймовірність того, що серед 400 випадкових відібраних деталей опиняться непровіреними від 70 до 100.

Тут n = 400, k=70, l=100, p = 0,2, q = 0,8. Тому в силу рівності (2.44), і згідно із (2.46),

Примітка. Зазначимо, що локальну та інтегральну граничні теореми Лапласа ще інколи називають локальною та інтегральною теоремами Мавра – Лапласа.

3.Розподілення випадкових похибок вимірювання. Нехай проводиться вимірювання деякої величини. Різниця х-а між результатом вимірювання х і справжнім значенням а вимірюваної величини називається похибкою вимірювання. Внаслідок впливу на вимірювання багатьох факторів, котрі неможливо врахувати (випадкові зміни температури, коливання приладу, помилки, котра виникає при заокругленні і т.д.), похибку вимірювання можна вважати сумою великого числа незалежних випадкових величин, яка по центральній граничній теоремі повинна бути розподілена нормально. Якщо при цьому нема систематично діючих факторів (наприклад, несправності приладів, підвищуючи прикожному вимірюванні показання), котрі призводять до систематичних похибок, то математичне сподівання випадкових похибок рівне нулю.

Отже, приймається положення: при відсутності систематичних діючих факторів похибка вимірювання є випадковою величиною(позначимо її через Т), розподіленою нормально, при чому її математичне сподівання рівне нулю, тобто щільність ймовірності величини Т рівна

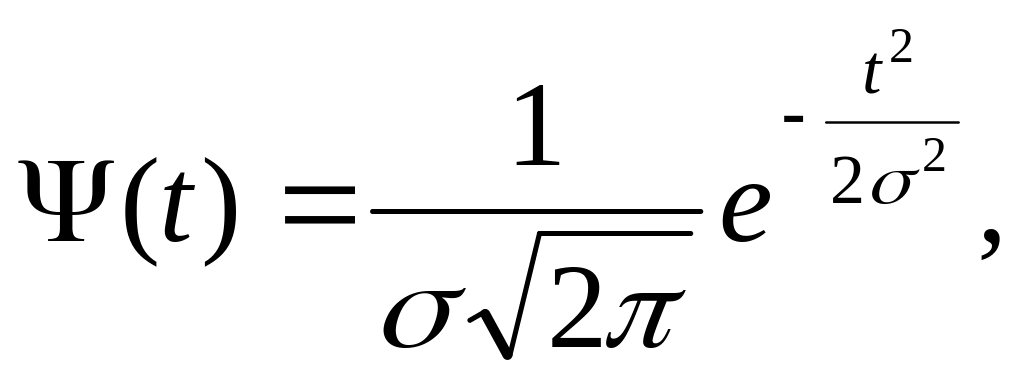
де σ – середнєквадратичне відхилення величини Т, що характеризує розкидання результатів вимірювань навколо вимірюваної величини.

Результати вимірювання також є випадковою величиною(позначимо її через Х), пов’язаною із т залежністю Х=а+Т. Звідси М(Х)=а, М(Х) = α, σ (Х) = σ (Т) = σ і Х має нормальний закон розподілу.

Помітимо, що випадкова похибка вимірювання, як і результати вимірювання, завжди виражаються в деяких цілих одиницях, пов’язаних із кроком шкали вимірювального приладу; в теорії зручніше рахувати випадкову похибку неперервною випадковою величиною, що полегшує розрахунки.

При вимірюванні можливі дві ситуації:

а)відомо σ (це характеристика приладу і комплексу умов, при котрих проводяться вимірювання), потрібно по результатах оцінити а;

б) σ не відома, потрібно по результатам вимірювань оцінити а і σ.

Розгляду цих ситуацій при проведенні фізичних дослідів буде присвячений § 4.3

Вправи

1.Нехай випадкова величина Х – число очок, випавших при підкиданні гральної кістки. Знайдіть закон розподілу випадкової величини Х

X	1	2	3		4	5	6
р	1/6	1/6	1/6	1/6		1/6	1/6

2.В грошовій лотереї випущено 100 квитків. Розігруються 1 виграш в 500 грн. та 10 виграшів по 10 грн. Знайдіть закон розподілу випадкового виграшу Х для володаря одного лотерейного квитка.

X	0	10	500
p	0,89	0,1	0,01

3. Закон розподілу випадкової величини Х заданий таблицею:

X	1	2	3
р	0,3	0,2	0,5

Знайдіть математичне сподівання випадкової величини Х. [2,2]

4. Знайдіть математичне сподівання виграшу Х у вправі 2.

[6 р.]

5. Знайдіть математичне сподівання випадкової величини Х, знаючи закон її розподілу:

X	2	3	5
р	0,3	0,1	0,6

[3,9]

6. Проводяться два постріли із ймовірностями попадання в ціль, рівними p₁ = 0,4; p₂ = 0,3. Знайдіть математичне сподівання загального числа влучень.

[0,7]

7. Знайдіть математичне сподівання суми числа очок, котрі можуть випасти при одному кидку двох гральних кісток.

[7]

8. Знайдіть математичне сподівання добутку числа очок, котрі можуть випасти при одному кидку двох гральних костей.

[12,25]

9.Незалежні випадкові величини Х та Y задані наступними законами розподілу:

X	2	4	5
р	0,1	0,3	0.6

та

У	1	9
p	0,8	0,2

Знайдіть математичне сподівання величини XY.

[32,56]

10.Знайдіть дисперсію випадкової величини Х, ктра задана наступним законом розподілу:

X	1	2	5
р	0,3	0,5	0,2

[2,01]

1 1.Відомі дисперсії двох незалежних випадкових величин Х та Y:

Знайдіть дисперсію суми цих величин.

[7]

12. Дисперсія випадкової величини х рівна 5. Знайдіть дисперсію наступних величин: а)X-1; б) -2Х; в)3X+6.

[а) 5; б) 20; в) 45]

13-15. Знайдіть математичне сподівання та дисперсію випадкових величин, заданих різними законами розподілу:

13.

X	-2	-1	0	1	2
р	0,1	0,2	0,3	0,3	0,1

14.

X	1	3	4	6	7
р	0,1	0,1	0,3	0,4	0,1

15.

х	5	7	10	15
р	0,2	0,5	0,2	0,1

16. До випадкової величини добавили сталу а. Як при цьому зміниться її: а)математичне сподівання; б)дисперсія?

[а)добавиться;б)не зміниться]

17.Випадкову величину помножили на а. Як при цьому зміняться:

а)математичне сподівання; б)дисперсія?

[а)помножиться на а; б)помножиться на а² ]

18. Випадкова величина Х приймає тільки два значання: 1 і -1, кожне із ймовірністю 0,5. Знайти дисперсію D(Х) та середнє квадратичне відхилення σ(Х).

[D(X) = 1; σ(x)=1]

19. Дисперсія випадкової величини D(Х) = 6,25. Знайдіть середнє квадратичне відхилення σ(Х).

[2,5]

20. Нехай закон розподілу випадкової величини х заданий таблицею:

X	4	10	20
p	1/4 _______	1/2	1/4

Визначте математичне сподівання М(Х), дисперсію D(Х) та середнє квадратичне відхилення σ(Х).

[M(X)=11;D(X)=33;σ(X)≈5,75]

21. Дискретна випадкова величина Х задана законом розподілу:

X	3	5
р	0,2	0,8

Знайдіть початкові моменти першого і другого порядків.

[ν1=4,6; ν2 = 21,8]

22. Дискретна випадкова величина Х задана законом розподілу, наведеним в попередньому прикладі. Знайдіть центральний момент другого порядку.

[μ₂ = 0,64]

23. Випадкова величина Х задана функцією розподілу:

0 при x≤-1

F(x)= при -1

1. при x>2

Знайдіть ймовірність того, що в результаті випробування випадкова величина Х набуде значення, що міститься в інтервалі (0;1).

[ ]

24.Випадкова величина Х задана повністю функцією розподілу:

0 при x≤2

F(x)= при 2<x≤4

1 при x>4

Знайти ймовірність того, що в результаті випробування Х набуде значення, що міститься в інтервалі (2;3)

[0,5]

25. Випадкова величина Х задана щільністю ймовірності

0 при x<0

f(x)= при 0≤x≤4

0 при x>4

Знайдіть ймовірність попадання випадкової величини Х на відрізку

[-2; 3].

[ ]

26. Щільність ймовірності випадкової величини Х задана виразом

Знайдіть ймовірність того, що величина Х попаде на інтервал (-1; 1).

[0,5]

27.Випадкова величина задана щільністю ймовірності

0 при x<-

f(x)= α cos x при - ≤x≤

0 при x>

Знайдіть коефіцієнт а.

[а = 0,5]

28. Дана диференціальна функція розподілу безперервної випадкової величини X

Знайдіть інтегральну функцію розподілу F(x).

28. Дана диференціальна функція розподілу безперервної випадкової величини X

Знайдіть інтегральну функцію розподілу F(x).

28. Функція

є щільністю ймовірності випадкової величини X. Знайдіть коефіцієнт А і функцію розподілу F(x).

28. Знайдіть математичне сподівання випадкової величини X, що задана щільністю ймовірності

28. Випадкова величина X задана щільністю ймовірності

Знайдіть математичне сподівання і дисперсію випадкової величини X.

28. У бавовні 75% довгих волокон. Яка ймовірність того, що серед узятих навмання трьох волокон виявиться 2 довгі волокна?

28. За деяких умов стрільби ймовірність попадання в ціль дорівнює 1/3. Проводиться 6 пострілів. Яка ймовірність рівно двох попадань?

28. Гральна кістка кидається 5 разів. Знайдіть ймовірність того, що 2 рази з'явиться число очок, яке кратне трьом.

28. Монета підкидається 5 разів. Яка ймовірність того, що герб з'явиться не менше двох разів.

28. Нехай схожість насіння даної рослини складає 80%. Знайдіть ймовірність того, що з трьох посіяних насінин зійдуть: а) дві; б) не менше двох.

28. По мішені проводиться 3 постріли, причому ймовірність попадання при кожному пострілі дорівнює 0,8. Розглядається випадкова величина X – число попадань в мішень. Знайдіть закон її розподілу.

X	0	1	2	3
p	0,008	0,096	0,384	0,512

28. Приймаючи ймовірність народження хлопчика і дівчинки однаковими, знайдіть ймовірність того, що серед чотирьох новонароджених - 2 хлопчики.

28. Ймовірність попадання в ціль при стрільбі із рушниці p=0,6. Знайдіть математичне сподівання загальної кількості попадань, якщо проводять 10 пострілів.

[6 попадань]

28. Знайдіть математичне сподівання кількості лотерейних квитків, на яку випадуть виграші, якщо придбано 20 квитків, причому ймовірність виграшу по одному квитку дорівнює 0,3.

[6 квитків]

28. Знайдіть дисперсію випадкової величини X – числа появ події А в 100 незалежних випробуваннях, в кожному з яких ймовірність настання події А дорівнює 0,7.

[21]

28. Знайдіть: а) математичне сподівання і б) дисперсію числа бракованих виробів в партії з 5000 виробів, якщо кожний виріб може бути бракованим з ймовірністю 0,02.

[а) 100 виробів; б) 98]

28. Проводиться 10 незалежних випробувань, в кожному з яких ймовірність появи події А рівна 0,6. Знайдіть дисперсію випадкової величини X – числа появи події А в цих випробуваннях.

[2,4]

28. Знайдіть дисперсію випадкової величини X – числа появи події А в двох незалежних випробуваннях, якщо M(X)=0,8.

[0,48]

28. Ріст дорослої жінки є випадковою величиною, розподіленою по нормальному закону з параметрами: а=164 см =5,5. Знайдіть щільність ймовірності цієї величини.

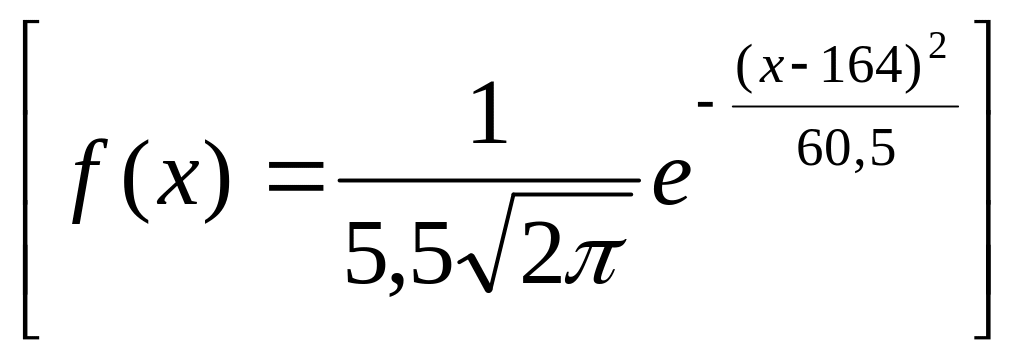
28. Випадкова величина X розподілена по нормальному закону. Математичне сподівання і середнє квадратичне відхилення цієї величини відповідно дорівнюють 0 і 2. Знайдіть ймовірність того, що X прийме значення, що належить інтервалу (-2; 3)

[0,77453]

28. Випадкова величина X розподілена по нормальному закону. Математичне сподівання і середнє квадратичне відхилення цієї величини відповідно дорівнюють 6 і 2. Знайдіть ймовірність того, що X прийме значення, що належить інтервалу (4; 8).

[0,6826]

28. Нехай маса спійманої риби підкоряється нормальному закону з параметрами: а=375 г; = 25 р. Знайдіть ймовірність того, що маса спійманої риби буде від 300 до 425 р.

[0,9759]

28. Діаметр деталі, що виготовляється в цеху, є випадковою величиною, розподіленою по нормальному закону. Дисперсія її рівна 0,0001, а математичне сподівання – 2,5 мм. Знайдіть межі, в яких з ймовірністю 0,9973 укладений діаметр навмання взятої деталі.

[2,47; 2,53]

28. Випадкова величина X розподілена по нормальному закону. Середнє квадратичне відхилення цієї величини дорівнює 0,4. Знайдіть ймовірність того, що відхилення випадкової величини X від її математичного сподівання по абсолютній величині буде менше 0,3.

[0,5468]

28. Випадкова величина X розподілена по нормальному закону. Середнє квадратичне відхилення цієї величини дорівнює 2. Знайдіть ймовірність того, що відхилення випадкової величини X від її математичного сподівання за абсолютною величиною буде менше 0,1.

[0,03988]

28. Випадкова величина X підкоряється нормальному закону розподілу з математичним сподіванням 30 і дисперсією 100. Знайдіть ймовірність того, що значення випадкової величини знаходиться в інтервалі (10; 50).

[0,954]

28. Знайдіть дисперсію випадкової величини X, заданою таблицею розподілу:

X	2	3	5
p	0,1	0,6	0,3

[1,05]

28. При виробленні деякої масової продукції ймовірність появи одного нестандартного виробу складає 0,01. Яка ймовірність того, що в партії зі 100 виробів цієї продукції 2 вироби будуть нестандартними?

[0,184]

28. На завод прибула партія деталей кількістю в 1000 шт. Ймовірність того, що одна деталь виявиться бракованою, рівна 0,001. Яка ймовірність того, що серед прибулих деталей буде 5 бракованих?

[0,003]

28. Гральну кістку кидають 80 разів. Визначте ймовірність того, що цифра 3 з'явиться 20 разів.

[0,0162]

28. При сталому технологічному режимі завод випускає в середньому 70% продукції першого сорту. Визначте ймовірність того, що з 1000 виробів число першосортних буде між 652 і 760.

[0,99945]

28. Ймовірність настання випадкової події при окремому випробуванні рівна p. Визначте ймовірність того, що в n випробуваннях подія наступить підряд k раз.

[(n – k+1) • p ^k • (1 – p)^n-k]

28. Підрахуйте при одночасному киданні n гральних кісток кількість результатів, в яких певна грань зустрічається k раз.

[5n-k ]

Двовимірні випадкові величини