2.6. Математичне сподівання і дисперсія нескінченої випадкової величини

Нехай нескінченна величина Х задана щільністю ймовірності f(x). Припустимо що всі можливі значення Х належать відрізку [a;b]. Точками x розіб’ємо на n часткових відрізків, довжини яких позначимо через , . Найбільшу з цих довжин позначимо через .

Припускаючи визначити математичне сподівання нескінченної випадкової величини по аналогії з дискретною, складемо суму

[нагадаємо, що похідні f(x при малих наближено дорівнюють ймовірності влучення випадкової величини Х в інтервал(x див.

§2.5, п.2]. Перейшовши в цій сумі до границі при отримаємо визначений интеграл , котрий і називають математичним сподіванням нескінченної випадкової величини Х, всі можливі значення якої належать відрізку [a;b]: M(X)=

Якщо всі можливі значення нескінченної випадкової величини Х належать всій числовій осі, то математичне сподівання визначається інтегралом

M(X)=

При цьому передбачається, що невласний інтеграл абсолютно сходиться, т.і. інтеграл , існує.

По аналогії з дисперсією дискретної випадкової величини визначається і дисперсія нескінченної випадкової величини.

Дисперсією нескінченної випадкової величини Х називається математичне сподівання квадрата її відхилення. Якщо всі можливі значення Х належать відрізку [a;b], то D(X)=

Якщо всі можливі значення Х належать всій числовій осі, то

D(X)= ,

при умові, що останній невласний інтеграл не сходиться.

Відзначимо, що властивості математичного сподівання і дисперсії дискретних випадкових величин зберігаються і для нескінченних випадкових величин.

Отже, для нескінченної величини Х середнє квадратичне відхилення визначається,як для дискретної величини, формулою

П р и к л а д. Нехай випадкова величина Х задана щільністю ймовірності

Визначимо математичне сподівання, дисперсію і середнє квадратичне відхилення Х.

Згідно з формулами (2.18) і (2.19), маємо

M(X)=

D(X)=

І, нарешті,

2.7.Основні закони розподілу нескінченних випадкових величин

1.Рівномірний розподіл. Розподіл ймовірностей нескінченої випадкової величини Х, приймаючи всі свої значення з відрізку [a;b], називається рівномірним, якщо її щільність ймовірності на цьому відрізку постійна, а зовні дорівнює нулю, тобто

Звідси

(2.20)

Але як відомо (див.§ 2.5, п.2) ,

(2.21)

З порівняння рівностей (2.20) і (2.21)отримаємо c=

Так, щільність ймовірності нескінченної випадкової величини Х, розподілено рівномірно на відрізку [a;b], має вигляд

П р и к л а д. На відрізку [a;b] навмання вказують точку. Яка ймовірність того,що ця точка виявиться у лівій частині відрізку?

Позначимо через Х випадкову величину, яка дорівнює координаті вибраної точки. Х розподілена рівномірно, а так як середина відрізку [a;b], має координату , то шукана ймовірність дорівнює (див.§ 2.5,п.2)

P(a<X<

Між іншим , цей результат був відомий з самого початку (див.§1.2, п.1).

2.Нормальний закон розподілу. Закон розподілу ймовірностей нескінченної випадкової величини Х називаеться нормальним законом , або законом Гаусса якщо її щільність ймовірності є

f(x)= (2.22)

де і a-сталі, причому .

Впевнимося, що функція (2.22) задовольняє умову (2.17). Дійсно перейшовши в інтегралі

(2.23)

до нової змінної

t= (2.24)

отримаємо інтеграл

Але

(див.додаток 1).

Звідси,

(2.25)

Значить інтеграл (2.23) також дорівнює одиниці.

Покажемо, що M(X)=a, або =D(x).Згідно з формулою(2.18), маємо M(X)= dx.

Ввівши нову змінну t по формулі (2.24), враховуючи рівність(2.25) отримаємо M(X)= )e dt+ dt=a- e / =a.

Потім, згідно з формулою (2.19)

D(X)= e- dx.

Використавши підстановку(2.24), отримаємо:

D(X)=

Застосовуючи тут метод інтегруваня частинами(t=u, te dt=dv), отримаємо з урахуванням (2.25)

D(X)=-

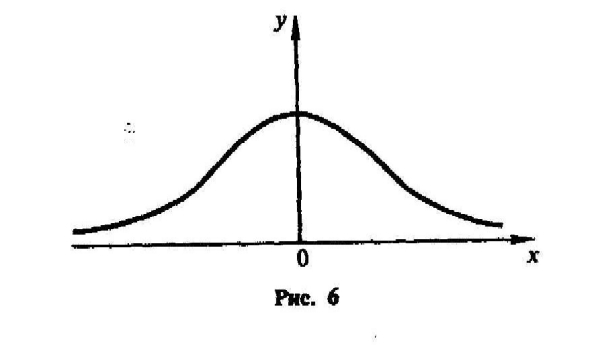
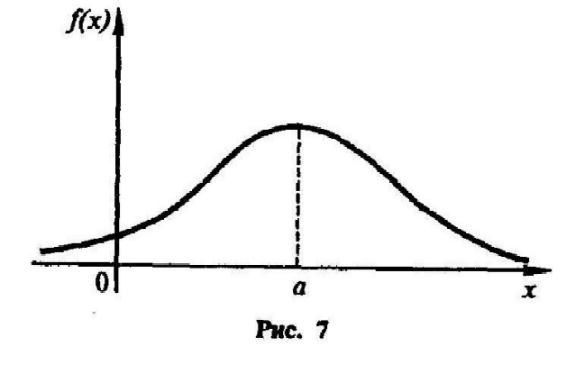
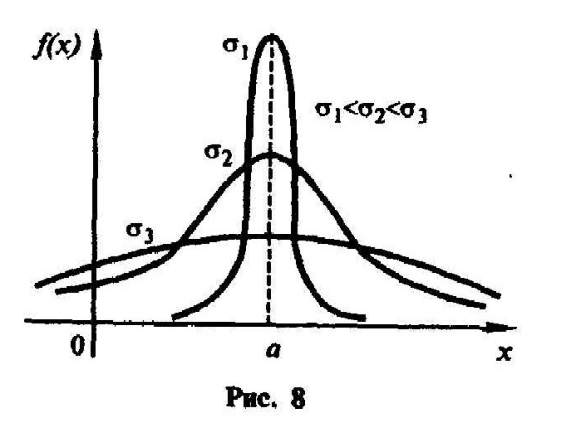
Графік функції (крива Гаусса) має вигляд (рис 6). З врахуванням графіка цієї функції графік функції (2.22) буде мати вигляд (рис.7). Причому його максимальна ордината дорівнює 1/( ). Значить ця ордината спадає з зростанням значення (крива „розтягується” до осі Ох-рис.8) і зростає (крива „зжимається” в додатньому напрямку осі Оу). Зміни значення параметру а (при незмінному значенні не впливають на форму кривої.

Нормальний розподіл з параметрами а=0 та називається нормованим. Щільність ймовірності в випадку такого розподілу виявляється

Ймовірність влучення випадкової величини, розподіленої по нормальному закону, в заданий інтервал.

Нехай випадкова величина Х розподілена по нормальному закону.Тоді ймовірність того що, Х прийме значення, що належить інтервалу ( ),згідно теоремі з п.2 параграфу 2.5.

P( <X< =

Зробивши в цьому інтегралі заміну змінної, , t= отримаємо P( <X< =

Враховуючи, що функція являється першопочатковою для і використовуючи формулу Ньютона-Лейбніца, будемо мати

(2.26)

П р и к л а д 1.Нехай випадкова величина Х розподілена по нормальному закону з параметрами a=30 та .Знайдемо ймовірність того, що Х прийме значення, що належить інтервалу (10;50).

Використовуючи формулу (2.26), отримаємо

P(10<X<50)=

По таблиці додатку 3 знаходимо .Звідси шукана ймовірність

P(10<X<50)=2 =0,9544.

Обрахування ймовірності заданого відхилення.

Часто потрібно визначити ймовірність того, що відхилення нормально розподіленої випадкової величини Х від її математичного сподівання по абсолютній величині менше заданого додаткового числа ,т.і. потрібно знайти P(

Використовуючи формулу (2.26) і враховуючи що функція непарна, маємо

P( т.е

P(

П р и к л а д 2. Нехай випадкова величина Х розподілена по нормальному закону з параметрами a=20 і Знайдемо P(

Використовуючи вираз (2.27) маємо

P(

По таблиці додатку 3 знаходимо .Тому P( .

Правило трьох сигм.

Використавши вираз (2.27) отримаємо P(

Але (див.таблицю додатку 3) і , значить, P( (2.28).

Формула (2.28) означає, що подія, перебуваючи в виконанні нерівності має ймовірність, наближену до одиниці,т.і. являється майже достовірною . Ця формула виражає так зване правило трьох сигм: якщо випадкова величина розподілена по нормальному закону розподілу, то модуль її відхилення від математичного сподівання не перевищує потроєного середнього квадратичного відхилення.

В кінці відмітимо, що нормальний розподіл ймовірностей має в теорії ймовірностей більше значень. Нормальному закону відповідає ймовірність при стрільбі в одну ціль, його використовують в теорії похибок фізичних вимірів і т.д.