122

РОЗДІЛ I

Випадкові події та ймовірності

§ 1.1. Випадкові події. Класичне визначення ймовірності

1. Поняття про випадкову подію. Досвід, експеримент, спостереження явища називають випробуванням. Випробуваннями, наприклад, є: кидання монети, постріл із гвинтівки, кидання гральної кістки (кубика з нанесеним на кожну грань числом очок - від одного до шести).

Результат випробування називається подією. Подіями є: випадання герба або цифри, влучення в ціль або промах, появу того або іншого числа очок на кинутій гральній кістці.

Для позначення подій викорисовуються великі букви латинського алфавіту: А, В, С і т.д.

Визначення 1. Дві події називаються сумісними, якщо поява однієї з них не виключає появи іншої в тому самому випробуванні.

Приклад 1. Випробування: однократне кидання гральної кістки. Подія А— поява чотирьох очок, подія В — появу парного числа очок. Події А і В сумісні.

Визначення 2. Дві події називаються несумісними, якщо поява однієї з них виключає появу іншої в тому самому випробуванні.

Приклад 2. Випробування: однократне кидання монети. Подія А — випадання герба, подія В— випадання цифри. Ці події несумісні, тому що поява однієї з них виключає появу іншої.

Несумісність більш ніж двох подій у даному випробуванні означає їхню попарну несумісність.

Приклад 3. Випробування: однократне кидання гральної кістки. Нехай події А₁ , А₂ , А₃ , А , А₅, А₆ — відповідно випадання одного очка, двох, трьох і т.д. Ці події є несумісними.

Визначення 3. Дві події А і В називаються протилежними, якщо в даному випробуванні вони несумісні й одна з них обов'язково відбувається.

Подію, протилежну події А, позначають через .

Приклад 4. Випробування: однократне кидання монети. Подія А — випадання герба, подія В— випадання цифри. Ці події протилежні, тому що результатами кидання можуть бути лише вони і поява одного з них виключає появу іншого, тобто А = або =В.

Визначення 4. Подія називається достовірною, якщо в даному випробуванні вона є єдино можливим її результатом, і неможливою, якщо в даному випробуванні вона свідомо не може відбутися.

Приклад 5. Випробування: витяг кулі з урни, у якій всі кулі білі. Подія А — виймуть білу кулю — достовірна подія; подія В — виймуть чорну кулю — неможлива подія.

Помітимо, що достовірна й неможлива події в даному випробуванні є протилежними.

Визначення 5. Подія А називається випадковою, якщо вона об'єктивно може наступити або не наступити в даному випробуванні.

Приклад 6. Подія А₆ — випадання шести очок при киданні гральної кістки — випадкова. Вона може наступити, але може й не наступити в даному випробуванні.

Приклад 7. Подія А₉₈ — проростання дев'яноста восьми зерен пшениці зі ста — випадкова. Ця подія може наступити, але, може бути, проросте зерен більше або менше.

2. Алгебра подій.

Визначення 1. Сумою подій A і В називається подія С = А + В, що полягає в настанні принаймні однієї з подій А або В.

Приклад 1. Випробування: стрілянина двох стрільців (кожний робить по одному пострілі). Подія А — влучення в мішень першим стрільцем, подія В — влучення в мішень другим стрільцем. Сумою подій А і В буде подія С=А+В, що полягає у влученні в мішень принаймні одним стрільцем.

Аналогічно сумою кінцевого числа подій А , А₂, ..., А_к називається подія А = А +А₂ +... + A_к, що складається в настанні хоча б однієї з подій А (і=1, ..., к).

З визначення 1 безпосередньо випливає, що А + В = В + А. Справедлива також і сполучна властивість. Однак А+А=А (а не 2А, як в алгебрі).

Визначення 2. Добутком подій А і В називається подія С=АВ, що полягає в тому, що в результаті випробування відбулися і подія А, і подія В.

Аналогічно добутком кінцевого числа подій А , А₂, …, A називається подія А = А А₂... А_к, що полягає у тому, що в результаті випробування відбулися всі зазначені події.

В умовах попереднього приклада добутком подій А і В буде подія С=АВ, що полягає у влученні в мішень двома стрільцями.

З визначення 2 безпосередньо випливає, що АВ = ВА.

Справедливі також сполучний і дистрибутивний закони. Однак АА = А (а не А^г).

3. Класичне визначення ймовірності. Усяке випробування спричиняє деяку сукупність результатів - результатів випробування, тобто подій. У багатьох випадках можливо перелічити всі події, які можуть бути результатом даного випробування.

Визначення 1. Говорять, що сукупність подій утворить повну групу подій для даного випробування, якщо його результатом обов'язково стає хоча б одне з них.

Приклади повних груп подій - випадання герба й випадання цифри при одному киданні монети; влучення в ціль й промах при одному пострілі; випадання одного, двох, трьох, чотирьох, п'яти й шести очок при одному киданні гральної кістки.

Розглянемо повну групу попарно несумісних подій U₁ ,U₂, ..., U_n,, пов'язану з деяким випробуванням. Припустимо, що в цьому випробуванні здійснення кожного з подій U (і= 1, 2, ..., п) рівноможливо, тобто умови випробування не створюють переваг у появі якої-небудь події перед іншими можливими.

Визначення 2. Події U U₂, ..., U_n, що утворять повну групу попарно несумісних і рівноможливих подій, називають елементарними подіями.

Приклад 1. Повернемося до досвіду з підкиданням гральної кістки. Нехай U — подія, що полягає в тім, що кістка випала гранню із цифрою і. Як ми вже відзначали (п. 1, 3), події U₁ U₂, ..., U , утворять повну групу попарно несумісних подій. Так як передбачається, що кістка однорідна й симетрична, то події U₁ U₂, ..., U , є й рівноможливими, тобто елементарними.

Визначення 3. Подія А сприяє події В, якщо настання події А спричиняє настання події В.

Приклад 2. Нехай при киданні гральної кістки події U₂, U₄ й U₆ — поява відповідно двох, чотирьох і шести очок, а А — подія, що полягає в появі парного числа очок; події U₂, U₄ й U₆ сприяє події А.

Визначення 4. (класичне визначення ймовірності). Ймовірністю Р(А) події А називається відношення т/п числа елементарних подій, сприяючих події А, до числа всіх елементарних подій, тобто

Р(А) = т/п.

Приклад 3. Обчислимо ймовірність випадання герба при одному киданні монети. Очевидно, подія А — випадання герба — і подія В-випадання цифри — утворять повну групу несумісних і рівноможливих подій для даного випробування. Виходить, тут п = 2. Події А сприяє лише одне подія - саме А, тобто тут m=1. Тому Р(А) = .

Приклад 4. Очевидно, що при одному киданні гральної кістки (ймовірність випадання якої-небудь цифри від 1 до 6 буде дорівнювати

P(U ) = , i=l, 2, ..., 6.

Приклад 5. Знайдемо ймовірність того, що при однократному киданні гральної кістки випаде число очок, що ділиться на 2 (подія А).

Число елементарних подій тут 6. Число спиятливих елементарних події 3 (випадання 2, 4 й 6). Тому

Приклад 6. При складанні команди космічного корабля виникає питання про психологічну сумісність окремих членів екіпажа. Допустимо, що треба скласти команду із трьох чоловік: командира, інженера й лікаря. На місце командира є три кандидати: а₁ , а₂ , a₃; на місце інженера — чотири кандидати: b , b₂, b , b , на місце лікаря -два кандидата: С₁, С₂. Проведена перевірка показала психологічну несумісність командира а₂ з інженерами b₃ b₄ і з лікарем С₂, а також інженера b_г з лікарем с_г. Будемо для простоти вважати, що без обліку фактора несумісності всі варіанти складання команди рівноможливі. Яка в цьому випадку ймовірність того, що буде складений екіпаж, всі члени якого психологічно сумісні один з одним?

Представимо всі варіанти команди, при яких члени екіпажа сумісні один з одним у вигляді «дерева» (мал. 1). Число гілок цього дерева, тобто результатів, сприятливих події А, дорівнює 16, а загальне число можливих комбінацій за правилом добутку дорівнює 4∙ 3∙ 2 = 24. Шукана ймовірність

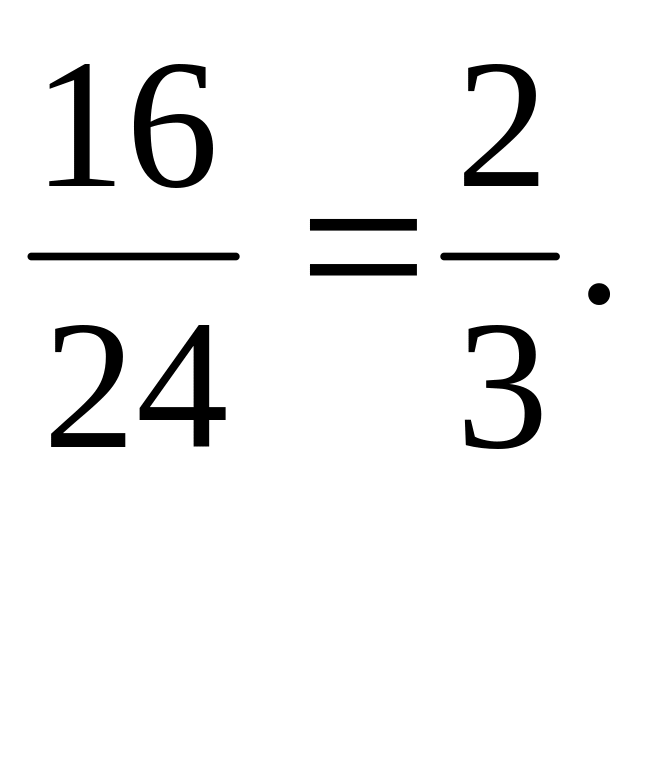
Задача (Ймовірності народження хлопчиків і дівчаток). Будемо припускати, що випадки народження хлопчика 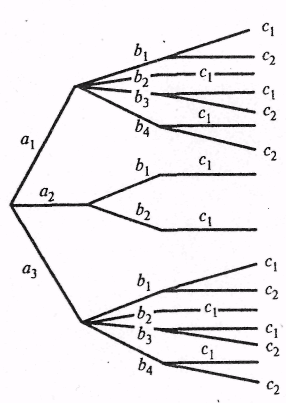й дівчинки — рівноможливі події.

Нехай у родині двоє дітей. Яка ймовірність, що обидві дитини - хлопчики? Якщо відомо, що один хлопчик, яка ймовірність, що обидві дитини - хлопчики?

На перше питання відповісти неважко. Є чотири рівних - можливих результати: ММ, МД, ДМ, ДД (М— хлопчик, Д— дівчинка). Результати МД і ДМ різні, тому що в першому з них спочатку народився хлопчик, а потім дівчинка, у другому — навпаки. Із цих чотирьох результатів тільки один ММ сприяє нашій події. Звідси слідує, що Р(ММ) =

Якщо додатково відомо, що одна дитина — хлопчик, то подія ДД виключається. Із трьох рівноможливих подій ММ, МД, ДМ як і раніше тільки одне ММ сприяє бажаному результату. Тому Р(ММ) =

Якщо відомо, що старша дитина— хлопчик, то виключаються результати ДМ і ДД. У цьому випадку Р(ММ) = .

З наведеного класичного визначення ймовірності випливають наступні її властивості:

1. Ймовірність достовірної події дорівнює одиниці. Дійсно, достовірній події повинні сприяти всі п елементарних подій, тобто т = п й, отже,

Р(А) = т/п = п/п = 1.

2. Ймовірність неможливої події дорівнює нулю.

Справді, неможливій події не може сприяти жодне з елементарних подій, тобто т = 0, звідки

Р(А) = т/п = 0/п = 0.

3. Ймовірність випадкової події є позитивне число, укладене між нулем й одиницею.

Дійсно, випадковій події сприяє лише частина із загального числа елементарних подій. Тому в цьому випадку 0<т<п й, виходить, 0<т/п<1. Отже, 0<Р(А)<1.

Таким чином, ймовірність будь-якої події задовольняє подвійну нерівність

0 Р(А) 1.

Зауваження. З визначення ймовірності слідує, що елементарні події є рівноможливими, тобто володіють однієї й тією же ймовірністю.