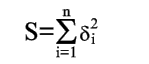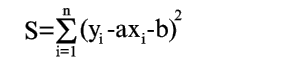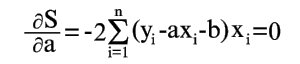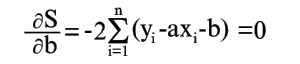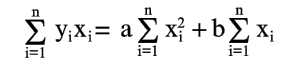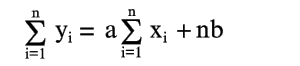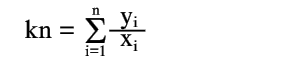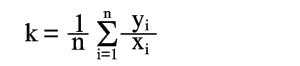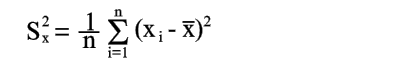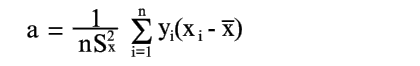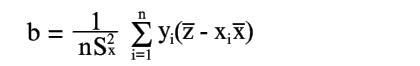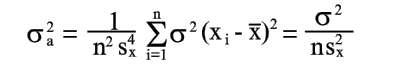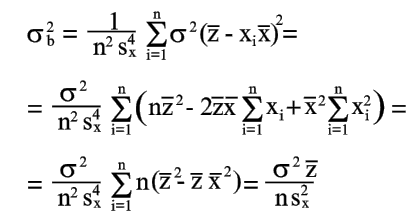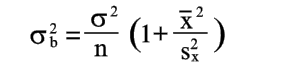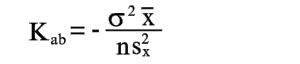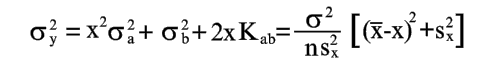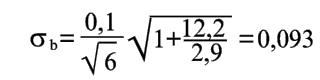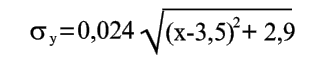Обобщенный мнк
Метод
наименьших квадратов допускает широкое
обобщение. Вместо минимизации суммы
квадратов остатков можно минимизировать
некоторую положительно определенную квадратичную
форму от
вектора остатков 
,
где 
—
некоторая симметрическая положительно
определенная весовая матрица. Обычный
МНК является частным случаем данного
подхода, когда весовая матрица
пропорциональна единичной матрице. Как
известно из теории симметрических
матриц (или операторов) для таких матриц
существует разложение 
.
Следовательно, указанный функционал
можно представить следующим образом 
,
то есть этот функционал можно представить
как сумму квадратов некоторых
преобразованных «остатков». Таким
образом, можно выделить класс методов
наименьших квадратов — LS-методы
(Least Squares).
Доказано
(теорема Айткена), что для обобщенной
линейной регрессионной модели (в которой
на ковариационную матрицу случайных
ошибок не налагается никаких ограничений)
наиболее эффективными (в классе линейных
несмещенных оценок) являются оценки
т. н. обобщенного
МНК (ОМНК, GLS — Generalized Least Squares) —
LS-метода с весовой матрицей, равной
обратной ковариационной матрице
случайных ошибок: 
.
Можно показать, что формула ОМНК-оценок параметров линейной модели имеет вид
Ковариационная матрица этих оценок соответственно будет равна
Фактически сущность ОМНК заключается в определенном (линейном) преобразовании (P) исходных данных и применении обычного МНК к преобразованным данным. Цель этого преобразования — для преобразованных данных случайные ошибки уже удовлетворяют классическим предположениям.
Взвешенный мнк
В
случае диагональной весовой матрицы
(а значит и ковариационной матрицы
случайных ошибок) имеем так называемый
взвешенный МНК (WLS — Weighted Least Squares). В
данном случае минимизируется взвешенная
сумма квадратов остатков модели, то
есть каждое наблюдение получает «вес»,
обратно пропорциональный дисперсии
случайной ошибки в данном наблюдении: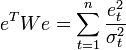 
.
Фактически данные преобразуются
взвешиванием наблюдений (делением на
величину, пропорциональную предполагаемому
стандартному отклонению случайных
ошибок), а к взвешенным данным применяется
обычный МНК.
История
До начала XIX в. учёные не имели определённых правил для решения системы уравнений, в которой число неизвестных меньше, чем число уравнений; до этого времени употреблялись частные приёмы, зависевшие от вида уравнений и от остроумия вычислителей, и потому разные вычислители, исходя из тех же данных наблюдений, приходили к различным выводам. Гауссу (1795) принадлежит первое применение метода, а Лежандр (1805) независимо открыл и опубликовал его под современным названием (фр. Méthode des moindres quarrés). Лаплас связал метод с теорией вероятностей, а американский математик Эдрейн (1808) рассмотрел его теоретико-вероятностные приложения. Метод распространён и усовершенствован дальнейшими изысканиями Энке, Бесселя, Ганзена и других.
Альтернативное использование мнк
Идея метода наименьших квадратов может быть использована также в других случаях, не связанных напрямую с регрессионным анализом. Дело в том, что сумма квадратов является одной из наиболее распространенных мер близости для векторов (евклидова метрика в конечномерных пространствах).
Одно из применений — «решение» систем линейных уравнений, в которых число уравнений больше числа переменных
,
где
матрица 
не
квадратная, а прямоугольная размера 
.
Такая
система уравнений, в общем случае не
имеет решения (если ранг
на
самом деле больше числа переменных).
Поэтому эту систему можно «решить»
только в смысле выбора такого вектора 
,
чтобы минимизировать «расстояние»
между векторами 
и 
.
Для этого можно применить критерий
минимизации суммы квадратов разностей
левой и правой частей уравнений системы,
то есть 
.
Нетрудно показать, что решение этой
задачи минимизации приводит к решению
следующей системы уравнений
Используя оператор псевдоинверсии, решение можно переписать так:
,
где 
—
псевдообратная матрица для
.
Данную задачу также можно «решить» используя взвешенный МНК, когда разные уравнения системы получают разный вес из теоретических соображений.
Естественно, данный подход может быть использован и в случае нелинейных систем уравнений.
Строгое обоснование и установление границ содержательной применимости метода даны А. А. Марковым и А. Н. Колмогоровым.
Теоретическое обоснование аппроксимации данных линейной функцией методом наименьших квадратов.
|
Для упрощения изложения рассмотрим сначала случай линейной функции одного аргумента. Пусть из опыта получены точки: |
x1, y1, |
|
|
x2, y2, ... |
|
(1) |
xn, yn |
|
|
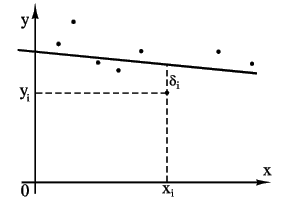
(см. рисунок). Требуется найти уравнение прямой
y=ax+b, |
(2) |
наилучшим образом согласующейся с опытными точками.
Пусть мы нашли
такую прямую. Обозначим через 
расстояние
опытной точки от этой прямой (измеренное
параллельно оси y).
Из уравнения (2) следует, что
|
(3) |
Чем меньше числа по абсолютной величине, тем лучше подобрана прямая (2). В качестве характеристики точности подбора прямой (2) можно принять сумму квадратов
|
(4) |
Покажем, как можно подобрать прямую (2) так, чтобы сумма квадратов S была минимальной. Из уравнений (3) и (4) получаем
|
(5) |
Условия минимума S будут
|
(6) |
|
(7) |
Уравнения (6) и (7) можно записать в таком виде:
|
(8) |
|
(9) |
Из уравнений (8) и (9) легко найти a и b по опытным значениям xi и yi. Прямая (2), определяемая уравнениями (8) и (9), называется прямой, полученной по методу наименьших квадратов (этим названием подчеркивается то, что сумма квадратов S имеет минимум). Уравнения (8) и (9), из которых определяется прямая (2), называются нормальными уравнениями.
Можно указать простой и общий способ составления нормальных уравнений. Используя опытные точки (1) и уравнение (2), можно записать систему уравнений для a и b
y1=ax1+b, |
|
|
y2=ax2+b, ... |
|
(10) |
yn=axn+b, |
|
|
Умножим левую и правую части каждого из этих уравнений на коэффициент при первой неизвестной a (т.е. на x1, x2, ..., xn) и сложим полученные уравнения, в результате получится первое нормальное уравнение (8).
Умножим левую и правую части каждого из этих уравнений на коэффициент при второй неизвестной b, т.е. на 1, и сложим полученные уравнения, в результате получится второе нормальное уравнение (9).
Этот способ получения нормальных уравнений является общим: он пригоден, например, и для функции
y=a0+a1x+a2x2+...+anxn. |
(11) |
Естественно, что здесь получится система из n+1 нормального уравнения для определения величин a0, a1, a2, ..., an.
Рассмотрим частный случай применения метода наименьших квадратов. Пусть из теории известно, что
k=y/x |
(12) |
есть величина постоянная и ее нужно определить по опытным данным (1).
Систему уравнений для k можно записать:
k=y1/x1, |
|
|
k=y2/x2, ... |
|
(13) |
k=yn/xn, |
|
|
Для получения нормального уравнения умножим каждое из этих уравнений на коэффициент при неизвестной k, т.е. на 1, и сложим полученные уравнения
|
(14) |
отсюда
|
(15) |
Следовательно, среднее арифметическое, полученное из опытных отношений yi/xi, дает решение поставленной задачи по методу наименьших квадратов. Это важное свойство средней арифметической объясняет ее широкое применение в практике обработки опытных данных.
Пример 1
На опыте получены значения x и y, сведенные в таблицу
x |
1 |
2 |
3 |
4 |
5 |
6 |
y |
5,2 |
6,3 |
7,1 |
8,5 |
9,2 |
10,0 |
Найти прямую (2) по методу наименьших квадратов.
Решение. Находим:
xi=21,
yi=46,3,
xi2=91,
xiyi=179,1.
Записываем уравнения (8) и (9) 91a+21b=179,1, 21a+6b=46,3, отсюда находим a=0,98 b=4,3.
Оценка точности метода наименьших квадратов
Дадим оценку точности метода для линейного случая, когда имеет место уравнение (2).
Пусть опытные
значения xi являются
точными, а опытные значения yi имеют
случайные ошибки с одинаковой
дисперсией 
для
всех i.
Введем обозначение
|
(16) |
Тогда решения уравнений (8) и (9) можно представить в виде
|
(17) |
|
(18) |
где |
|
|
(19) |
Из уравнения (17) находим |
|
|
(20) |
Аналогично из уравнения (18) получаем |
|
|
(21) |
так как |
|
|
(22) |
Из уравнений (21) и (22) находим |
|
|
(23) |
Уравнения (20) и (23) дают оценку точности коэффициентов, определенных по уравнениям (8) и (9).
Заметим, что коэффициенты a и b коррелированы. Путем простых преобразований находим их корреляционный момент.
|
(24) |
Уравнения (20), (23) и (24) позволяют найти оценку для ошибки y, которую дает уравнение (2) в произвольной точке x, если коэффициенты a и b найдены по уравнениям (8) и (9). Из уравнений (2), (20), (23) и (24) находим
|
(25) |
На основании уравнений (20), (23) и (25) можно сделать следующие выводы:
1.Точность коэффициентов a и b тем выше, чем больше sx, т.е. чем больше рассеивание опытных точек на оси x.
2.Точность
коэффициента b тем выше, чем меньше 
.
3.Ошибка уравнения
(2) наименьшая в точке, где 
,
и наибольшая в точках, где величина 
имеет
наибольшее значение.
Рассмотрим на примере использование уравнений (20)-(25).
Пример 2
Требуется оценить
точность решения примера 1 при 
.
Решение. В условиях этого примера имеем n=6.
=21/6=3,5,
sx2=91/6-(3,5)2=2,9.)
Из уравнений (20), (23) и (25) находим
|
|
|
|
|
|
Отсюда находим
=
0,072 при x=1 и 6,
=
0,041 при x=3,5.
Программная реализация аппроксимации данных линейной функцией методом наименьших квадратов
Начальный экран среды разработки. Среда разработки работает в режиме для программирования на C#.
Для создания нашего приложения выбираем File -> New -> Project
В появившемся окне выбираем Windows Forms Application.
При выборе этой опции среда сама создаст для нас шаблон для нашего Windows приложения с пользовательским интерфейсом.
Начальный шаблон формы, сгенерированный средой:
Сначала настроим нашу форму и добавим на неё необходимые нам элементы.
Делать это будем с помощью дизайнера форм - это вшитый в среду инструмент.
В параметрах формы переименуем её и установим минимальные размеры окна.
Минимальные размеры установим 517:467 пикселей. Изменим заголовок на "Метод наименьших квадратов". Добавим к форме зону для меню и создадим первое подменю "Файл". В него добавим два пункта : "демонстрация","из файла" и "Выход". Зададим для пункта меню комбинацию клавиш Ctrl + D.
Для генерации графиков на форме нам понадобиться объект типа PictureBox. На нем мы и будем рисовать наши графики. Зададим этому объекту размеры 400 на 400 и имя mnkDemonstrationPictureBox. В результате этих действий получим такую форму:
Теперь перейдем к программированию логики приложения.
Логика программы, связанная с реакцией на действия пользователя с формой, находиться в классе MainForm.ch . Логика отвечающая за отрисовку графика в классе Drawer.ch
Код класса MainForm.ch :
using System;
using System.Drawing;
using System.Windows.Forms;
namespace Kursovaya_MNK
{
public partial class MainForm : Form
{
Bitmap mnkDemonsrationBitMap;
Graphics mnkDemonstrationGraphics;
Drawer dr;
public MainForm()
{
InitializeComponent();
mnkDemonsrationBitMap = new Bitmap(mnkDemonstrationPictureBox.Width, mnkDemonstrationPictureBox.Height);
mnkDemonstrationGraphics = Graphics.FromImage(mnkDemonsrationBitMap);
}
private void demonstrationToolStripMenuItem_Click(object sender, EventArgs e)
{
dr = new Drawer(mnkDemonstrationGraphics);
dr.DrawFromRandomArray();
mnkDemonstrationPictureBox.Image = mnkDemonsrationBitMap;
}
private void exitToolStripMenuItem_Click(object sender, EventArgs e)
{
this.Close();
}
private void fromFileToolStripMenuItem_Click(object sender, EventArgs e)
{
string filePath = "";
OpenFileDialog openFileDialog1 = new OpenFileDialog() { Filter = "Текстовые файлы(*.txt)|*.txt" };
if (openFileDialog1.ShowDialog() == DialogResult.OK)
{
filePath = openFileDialog1.FileName;
dr = new Drawer(mnkDemonstrationGraphics);
dr.DrawFromFile(filePath);
mnkDemonstrationPictureBox.Image = mnkDemonsrationBitMap;
}
}
}
}
При запуске программы создается экземпляр класса MainForm.ch. Класс имеет два поля для работы с графикой - Bitmap mnkDemonsrationBitMap и Graphics mnkDemonstrationGraphics.
При создании экземпляра класса вызывается его конструктор. В нем сначало вызывается метод InitializeComponent() - это метод инициализирует на форме все элементы, которые мы добавили в дизайнере формы(см. выше). Код метода сгенерирован средой автоматически. В конструкторе класса мы инициализируем mnkDemonsrationBitMap пустой картинкой с размерами, соответствующими размерам нашего PictureBox на форме. Из этого пустого рисунка мы возьмем Graphics - объект, инкапсулирующий поверхность рисования. С этой графикой мы и будем работать.
В классе так же присутствуют три метода, отвечающие за реакцию на действия пользователя.
demonstrationToolStripMenuItem_Click(object sender, EventArgs e) отвечает за нажатие пользователем на кнопку "Демонстрация" в меню, а exitToolStripMenuItem_Click(object sender, EventArgs e) - на кнопку "Выход". При нажатии на кнопку выход форма просто закрывается командой this.Close().(ключевое слово this обращается к конкретному экземпляру объекта, на котором был вызван метод).
При нажатии на кнопку "Демонстрация" создается экземпляр класса Drawer, который отвечает за отрисовку всей графики. Для его создания необходимо ему передать параметр типа Graphics(поверхность, на которой нужно рисовать). На экземпляре Drawer вызывается метод DrawFromRandomArray();который и преображает переданную ранее этому объекту графику. Затем, эта графика передается на форму для отображения.
Метод fromFileToolStripMenuItem_Click(object sender, EventArgs e) отвечает за реакцию при нажатия кнопки "Из файла". Он открывает диалоговое окно выбора файла и если файл был выбран, то создает объект класса Drawer и вызывает метод DrawFromFile и передает ему адрес выбранного файла.
Код класса Drawer.ch :
using System;
using System.Drawing;
namespace Kursovaya_MNK
{
class Drawer
{
int fillHeight, fillWidth;
Graphics graf;
SolidBrush brush = new SolidBrush(Color.White);
public Drawer(System.Drawing.Graphics graphics)
{
this.graf = graphics;
fillHeight = (int) graf.VisibleClipBounds.Height;
fillWidth = (int) graf.VisibleClipBounds.Width;
}
public void DrawFromRandomArray()
{
Point[] points;
graf.FillRectangle(brush, new Rectangle(0, 0, fillWidth , fillHeight));
points = GeneratePointsArray(10);
DrawPointsArray(points);
CalcAndDrawLine(points);
}
public void DrawFromFile(String filePath) {
Point[] points;
graf.FillRectangle(brush, new Rectangle(0, 0, fillWidth, fillHeight));
points = GetPointsArrayFromFile(filePath);
DrawPointsArray(points);
CalcAndDrawLine(points);
}
private Point[] GetPointsArrayFromFile(String filePath) {
String[] fileStrings = System.IO.File.ReadAllLines(@filePath);
Point[] resultPointsArray = new Point[fileStrings.Length];
for (int i = 0; i < fileStrings.Length; i++ )
{
if(!fileStrings[i].Equals(null)){
String[] splittedStr = fileStrings[i].Split(' ');
resultPointsArray[i] = new Point( int.Parse(splittedStr[0]),
fillHeight - int.Parse(splittedStr[1]));
}
}
return resultPointsArray;
}
private Point[] GeneratePointsArray(int size)
{
Random random = new Random();
Point[] resultPointsArray = new Point[size];
for (int i = 0; i < size; i++)
{
resultPointsArray[i] = new Point( Convert.ToInt32(random.Next(fillWidth )),
fillHeight - Convert.ToInt32(random.Next(fillHeight )) );
}
return resultPointsArray;
}
private void DrawPointsArray(Point[] pointsArray)
{
Pen pen = new Pen(Color.Black, 3.0f);
for (int i = 0; i < pointsArray.Length; i++)
{
graf.DrawEllipse(pen, pointsArray[i].X,pointsArray[i].Y, 2, 2);
}
}
private void CalcAndDrawLine(Point[] points)
{
Pen pen = new Pen(Color.Red);
float summXi = 0, summXKvi = 0, summYi = 0, summXYi = 0, n = points.Length;
float coefA, coefB, x, x2;
foreach (Point point in points)
{
summXi += point.X;
summYi += point.Y;
summXKvi += point.X * point.X;
summXYi += point.X * point.Y;
}
coefA = (n * summXYi - summYi * summXi) / (n * summXKvi - summXi * summXi);
coefB = (summYi - coefA * summXi) / n;
x = 0;
x2 = fillWidth;
try
{
graf.DrawLine(pen, x, coefA * x + coefB, x2, coefA * x2 + coefB);
}
catch(Exception e){
graf.FillRectangle(brush, new Rectangle(0, 0, fillWidth, fillHeight));
graf.DrawString("Произошла ошибка при вычислениях! \n"+
"Вероятно, при вычислении коэффициента А была попытка деления на ноль \n"+
"Коэф. А: " + coefA + "\n" +
"Коэф. В: " + coefB,
new Font("a",10),
new SolidBrush(Color.Black),
new Point(10,10));
Console.Write(e.StackTrace);
}
}
}
}
При создании класса инициализируются его поля - графика для обработки, ширина и высота области для рисования. Класс содержит два публичных метода - DrawFromFile и DrawFromRandomArray. Один рисует массив случайных точек, другой рисует массив, который считывается из файла. Для удобства чтения кода функционал генерации случайного массива, считывания массива из файла, отрисовки массива точек и расчета и отрисовки аппроксимирующей линии выделены в отдельные приватные методы.
private Point[] GeneratePointsArray(int size) - приватный метод, который генерирует случайный массив точек и возвращает его. Точки здесь представляются экземплярами класса Point. Основная суть этого класса - поля X и Y (координаты). Метод создает массив точек переданного в параметрах метода размера, заполняет его случайными числами и возвращает этот массив. Массив заполняется в цикле for с помощью стандартного класса Random - генератора случайных чисел. Метод Next(int n) класса Random генерирует случайное число в диапазоне от нуля до n.
private void DrawPointsArray(Point[] pointsArray) - приватный метод, который рисует массив точек, переданный ему в параметрах. В цикле он проходит по каждой точке массива и наносит их на поверхность для рисования, полученную при инициализации Drawer, в виде эллипсов с одинаковыми осями.
private void CalcAndDrawLine(Point[] points) - приватный метод, который ищет уравнение аппроксимированной прямой по полученному в параметрах массиву точек и рисует эту прямую на всю ширину графики. Все расчеты коэффициентов происходят по приведенной выше теории. В метод включена обработка возможной ошибки программы.
private Point[] GetPointsArrayFromFile(String filePath) - метод, который считывает все строки из указанного файла и преобразует их в массив координат точек.
Заключение
После запуска файла Kurs.exe мы можем работать в программе.
Используя комбинацию Ctrl+D мы получим случайное множество точек:
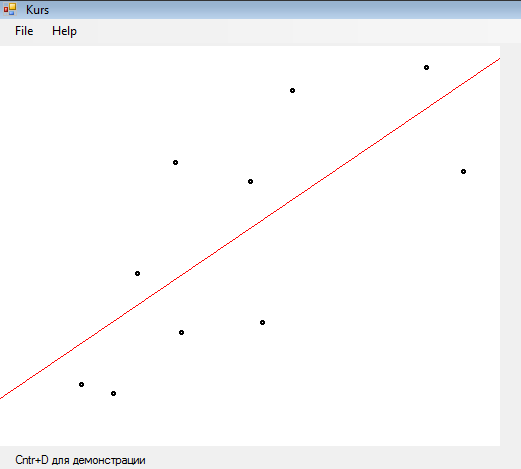
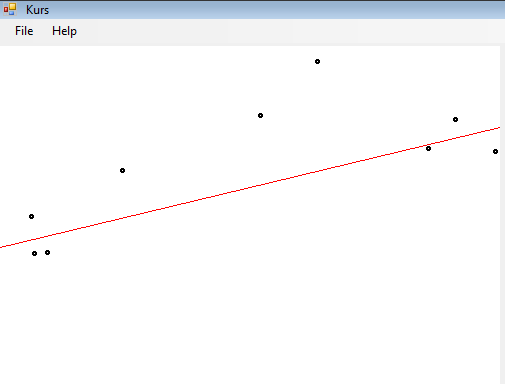
Используя кнопку «из файла» и задав файл, из которого читаем данные получим:
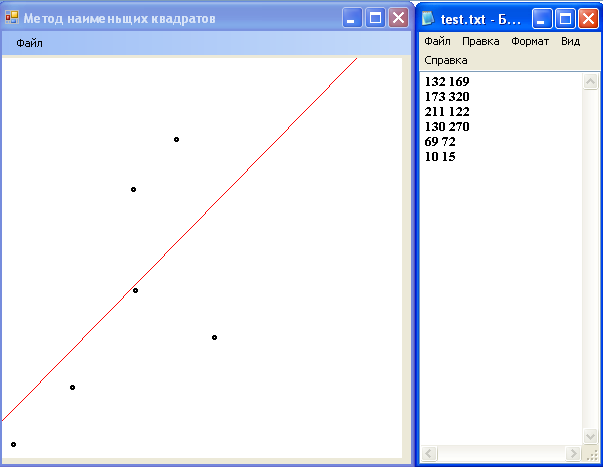
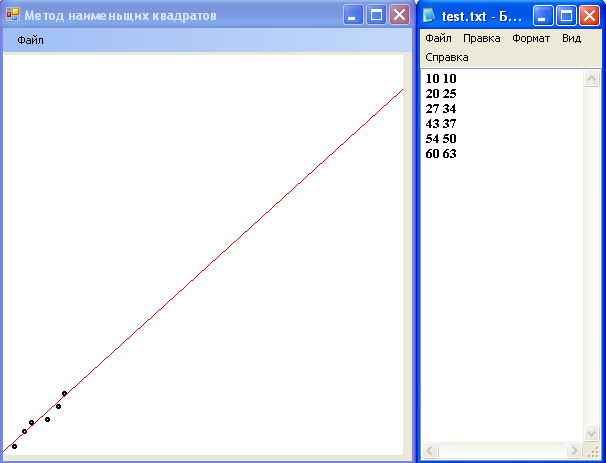
В данной работе была разработана программа, позволяющая аппроксимировать данные линейной функцией методом наименьших квадратов. При помощи языка С# получена программа, которая как видно из скриншотов, успешно справляется с построением прямой, максимально приближенной к массиву точек, который мы можем задавать как случайным образом, так и при помощи файла формата txt.
Литература
Линник Ю. В. Метод наименьших квадратов и основы математико-статистической теории обработки наблюдений. — 2-е изд. — М., 1962. (математическая теория)
Айвазян С. А. Прикладная статистика. Основы эконометрики. Том 2. — М.: Юнити-Дана, 2001. — 432 с. — ISBN 5-238-00305-6
Доугерти К. Введение в эконометрику: Пер. с англ. — М.: ИНФРА-М, 1999. — 402 с. — ISBN 8-86225-458-7
Кремер Н. Ш., Путко Б. А. Эконометрика. — М.: Юнити-Дана, 2003-2004. — 311 с. — ISBN 8-86225-458-7
Магнус Я. Р., Катышев П. К., Пересецкий А. А. Эконометрика. Начальный курс. — М.: Дело, 2007. — 504 с. —ISBN 978-5-7749-0473-0
Эконометрика. Учебник / Под ред. Елисеевой И. И. — 2-е изд. — М.: Финансы и статистика, 2006. — 576 с. —ISBN 5-279-02786-3
Александрова Н. В. История математических терминов, понятий, обозначений: словарь-справочник. — 3-е изд.. —М.: ЛКИ, 2008. — 248 с. — ISBN 978-5-382-00839-4
Шор. Я. Б. Статистические методы анализа и контроля качества.