2.4. Преобразование ортогональных проекций.

Содержание задания

(Правильные ответы отмечены «*»)

Задание 49

Методы преобразования ортогональных проекций предназначены для:

1) -

Лучшего понимания условий задачи;

2) -

Упрощения исходных графических данных задачи и оптимизации процесса её решения;

*

3) -

Проверки знаний;

4) -

Того, чтобы окончательно запутать студента.

Задание 50

Первой из задаваемых дополнительных плоскостей проекций при использовании метода замены плоскостей проекций обычно присваивают номер:

3

2

4 *

5

6

Содержание задания

(Правильные ответы отмечены «*»)

Задание 51

Проекции точки А после преобразования эпюра методом вращения обычно обозначаются:

1

2

3 *

4

Содержание задания

Правильный ответ

Задание 52

Порядок действий, осуществляемых при использовании метода вращения, следующий:

1 - ___, 2 - ___, 3 - ___.

а) – поворот объекта в положение, удобное для построений, когда прямые (или плоскости) проецируются в частном положении;

б) – выбор оси вращения;

в) – осуществление проецирования и получение графического результата.

1 - __(б)__,

2 - __(а)__,

3 - __(в)__.

Задание 53

Натуральная величина отрезка прямой на эпюре найдена методом:

вращения

треугольника

замены плоскостей проекций

четырёхугольника

1

2

3 *

4

Задание 54

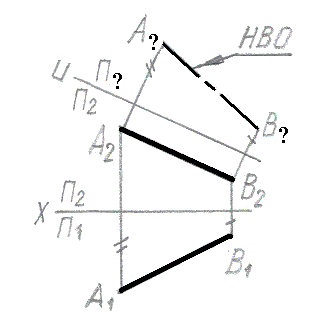
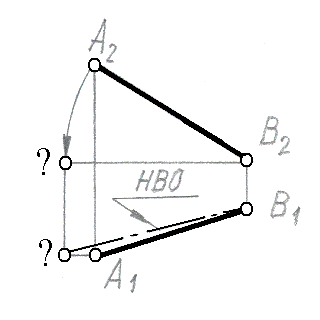
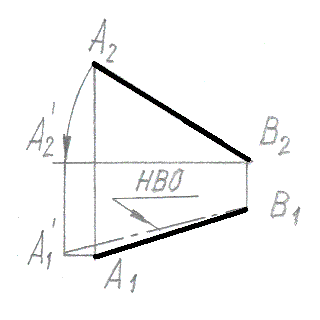
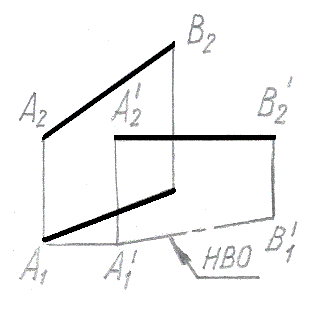
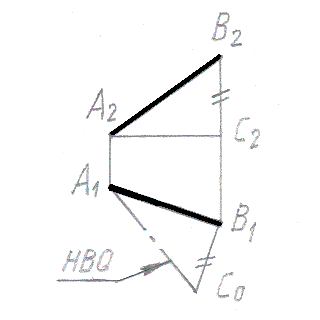
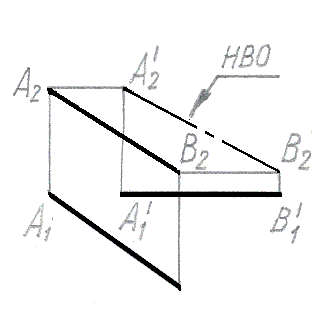
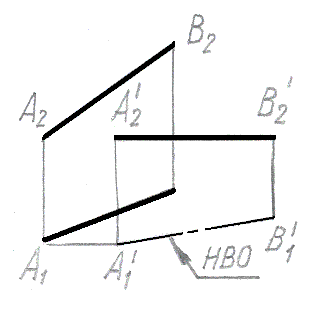
Метод прямоугольного треугольника использован для нахождения натуральной величины отрезка прямой на рис.:

1

2

3 *

4

Содержание задания

(Правильные ответы отмечены «*»)

Задание 55

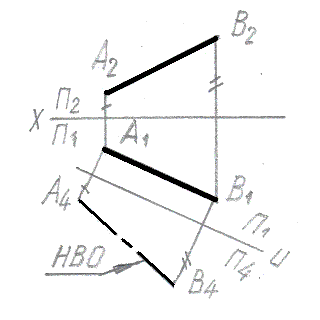
Метод замены плоскостей проекций использован для нахождения натуральной величины отрезка прямой на рис.:

1

2

3

4*

Содержание заданий

Варианты ответов

Задание 56

Метод нахождения натуральной величины отрезка прямой называется методом “______” треугольника.

прямоугольного

Задание 57

Метод нахождения натуральной величины отрезка прямой, при котором вводится дополнительная плоскость, называется методом “______” плоскостей проекций.

замены

Задание 58

Соответствие названий различных методов нахождения натуральной величины отрезка прямой и иллюстрирующих их эпюров

Правильный ответ

Метод

1 -

Вращения

2 -

Замены плоскостей проекций

3 -

Прямоугольного треугольника

1  В

2  Г

3  А

Эпюр

A

Б

В

Г