Дані взяти з таблиці 6

Таблиця 6

№ стовпця	1	2	3	4	5	6	7	8	9	0
№ схеми	1	2	3	4	5	6	7	8	9	10	е
Двотавр (швелер) №	10	20	14	16	18	20	22	24	27	30	в
Смуга: товщина, мм ширина, мм	4 40	6 60	8 100	10 80	12 100	14 40	16 160	18 60	20 120	25 200	г а

Задача 8 розрахунок балки при згині

На рисунках 8а і 8б наведені схеми балок.

Необхідно:

1. Для обох схем побудувати епюри поперечних сил та згинальних моментів.

2. Для схеми 8а підібрати сталеву балку двотаврового перерізу, використовуючи умову міцності за нормальними напруженнями. При розв’язуванні задачі прийняти .

3. Для схеми 8б підібрати дерев’яну балку прямокутного поперечного перерізу 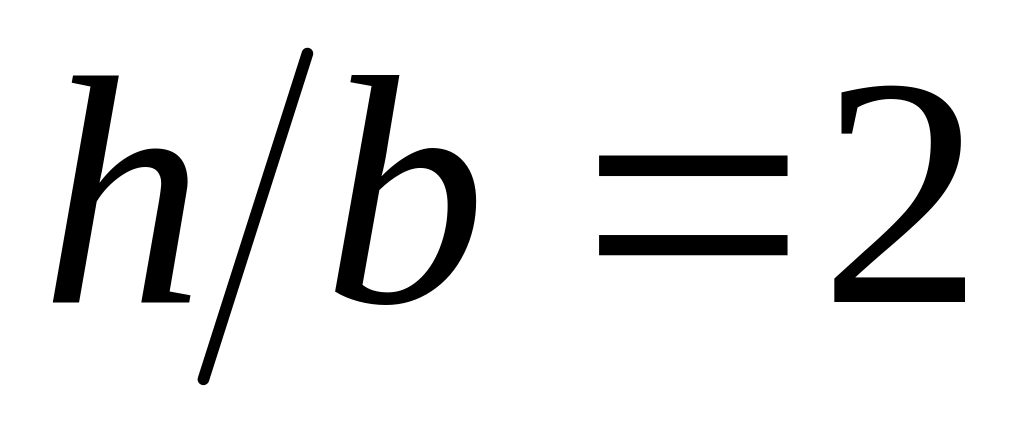. Прийняти, що допустиме напруження для дерева .

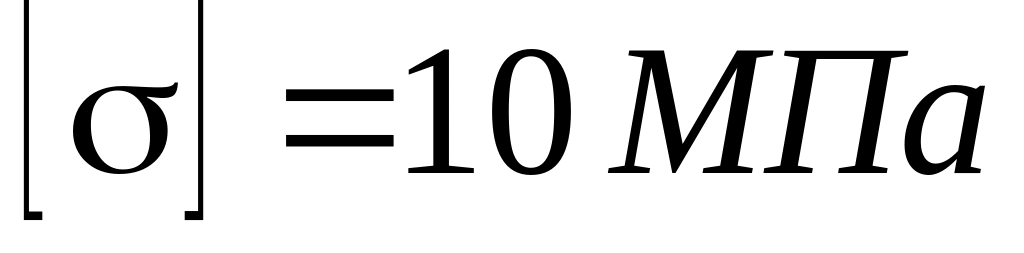4. Побудувати епюри нормальних напружень в небезпечних перерізах.

5. Для схеми 8б визначити максимальні дотичні напруження.

Примітка:

1. Дані для розв’язування задач взяти з таблиці 8.

2. Прийняти інтенсивність рівномірно розподіленого навантаження .

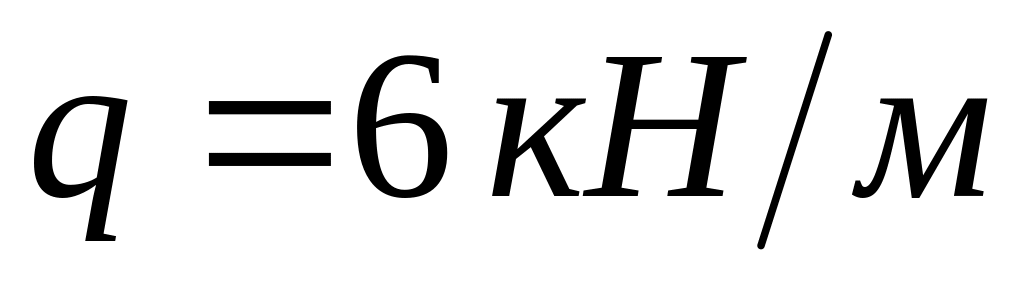Таблиця 8

№ рядка	№ схеми	а, м	Р, кН	М, кНм
1	1	2,0	10	4
2	2	1,8	12	6
3	3	1,6	14	8
4	4	1,4	10	10
5	5	1,2	12	4
6	6	1,0	15	6
7	7	1,2	8	8
8	8	1,4	10	10
9	9	1,6	12	4
0	10	1,8	14	6
	е	в	г	а

Рекомендована послідовність розв’язання задачі:

1. Застосувавши рівняння статики, визначити реакції в опорах.

2. Методом перерізів побудувати епюри поперечних сил та згинальних моментів.

3. З умови міцності при згині визначити осьовий момент опору, підібрати переріз.

Задача 9 розрахунок статично невизначуванної балки Для балки, яка зображена на рисунку 9

Необхідно:

1. знайти згинальний момент на лівій опорі (в долях );

2. побудувати епюри і ;

3. побудувати епюру прогинів, розрахувавши три ординати в прольоті і дві на консолі.

Таблиця 9

№ рядка	№ схеми
1	1	0,1	0,1
2	2	0,2	0,2
3	3	0,3	0,3
4	4	0,4	0,4
5	5	0,5	0,5
6	6	0,6	0,6
7	7	0,7	0,7
8	8	0,8	0,8
9	9	0,9	0,9
0	10	1,0	1,0
	е	б	в

Вказівки. Для відповіді на перше питання потрібно вибрати основну систему у вигляді вільно лежачої на двох опорах балки і скласти рівняння деформації, виражаючи думку, що сумарний кут повороту на лівій опорі від заданого навантаження і від опорного моменту дорівнює нулю.

Можна також розв’язувати задачу по іншому, склавши два рівняння:

1. рівняння статики у вигляді суми моментів всіх сил відносно правої опори;

2. рівняння метода початкових параметрів, використавши умову, що прогин на правій опорі дорівнює нулю.

З цих двох рівнянь можна знайти згинальний момент і реакцію на лівій опорі ( і ).

Для відповіді на третє питання доцільно використати метод початкових параметрів, оскільки два початкових параметри ( і ) відомі, а два інших ( і ) будуть знайдені в процесі виконання двох перших пунктів контрольної роботи.

При побудові епюр прогинів треба врахувати, що пружна лінія балки обернена опуклістю вниз там, де він від’ємний. Нульовим точкам епюри М відповідають точки перегину пружної лінії.

37