Задачі для контрольних робіт Задача 2

СТАТИЧНО НЕВИЗНАЧУВАННІ СИСТЕМИ

ПРИ РОЗТЯГУВАННІ-СТИСКАННІ

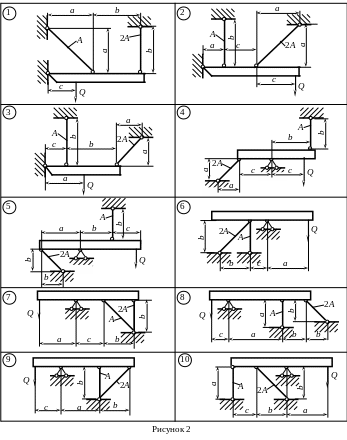
Абсолютно жорсткий брус спирається на шарнірно нерухому опору та є прикріплений до двох стержнів за допомогою шарнірів (рис. 2).

Необхідно:

1. знайти зусилля та напруження в стержнях, виразивши їх через силу ;

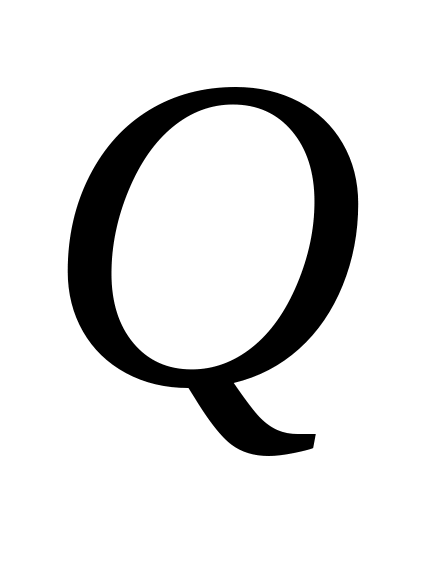2. знайти допустиме навантаження , прирівнявши найбільше з напружень в двох стержнях до допустимого напруження ;

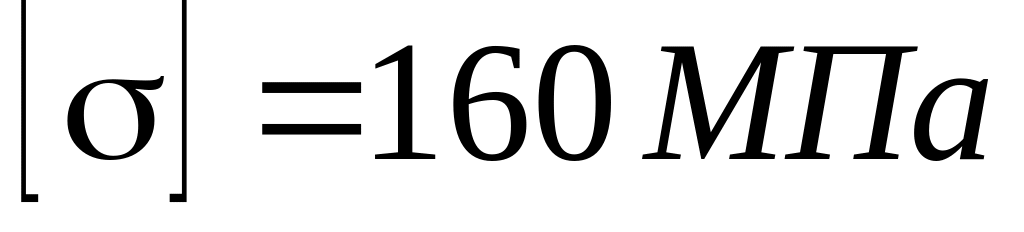3. знайти граничну вантажопідйомність системи та допустиме навантаження , якщо границя текучості 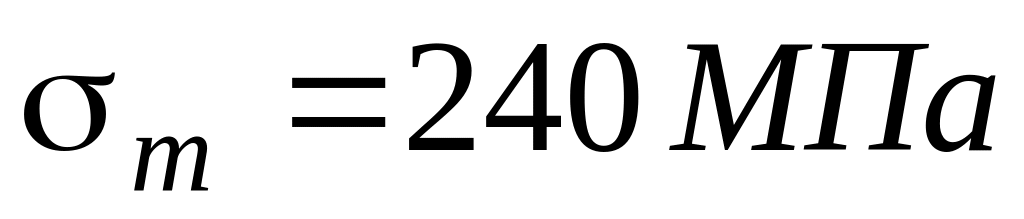та запас міцності ;

4. порівняти величини , отримані при розрахунку за допустимим напруженням (див.п. 2) та допустимим навантаженням (див.п. 3).

Дані взяти із таблиці 2.

Таблиця 2

№ рядка	Схема по рис. 2	А	a	b	c
			м
1	1	11	2,1	2,1	1,1
2	2	12	2,2	2,2	1,2
3	3	13	2,3	2,3	1,3
4	4	14	2,4	2,4	1,4
5	5	15	2,5	2,5	1,5
6	6	16	2,6	2,6	1,6
7	7	17	2,7	2,7	1,7
8	8	18	2,8	2,8	1,8
9	9	19	2,9	2,9	1,9
0	10	20	3,0	3,0	2,0
	е	в	г	д	е

Зауваження. Для визначення двох невідомих сил в стержнях треба скласти одне рівняння статики і одне рівняння деформацій.

Для відповіді на третє питання задачі треба мати на увазі те, що в одному з стержнів напруження більше, ніж в другому. При збільшені навантаження напруження в першому стержні досягає границі текучості раніше, ніж в другому. Коли це відбувається, напруження в першому стержні не буде деякий час зростати навіть при збільшенні навантаження, система стане нібито статично визначаємою, навантаженою силою Р (поки ще невідомою) та зусиллям в першому стержні:

. (1)

При подальшому збільшенні навантаження напруження і в другому стержні досягне границі текучості:

. (2)

Склавши рівняння статики та підставивши в нього значення зусиль (1) та (2), знайдемо із цього рівняння граничну вантажопідйомність .

Задача 4 плоский напружений стан

Сталевий кубик знаходиться під дією сил, які утворюють плоский напружений стан (одне з трьох головних напружень рівне нулю).

Необхідно знайти:

1. головні напруження і положення головних площадок;

2. максимальні дотичні напруження і положення площадок, де діє ;

3. відносні деформації ;

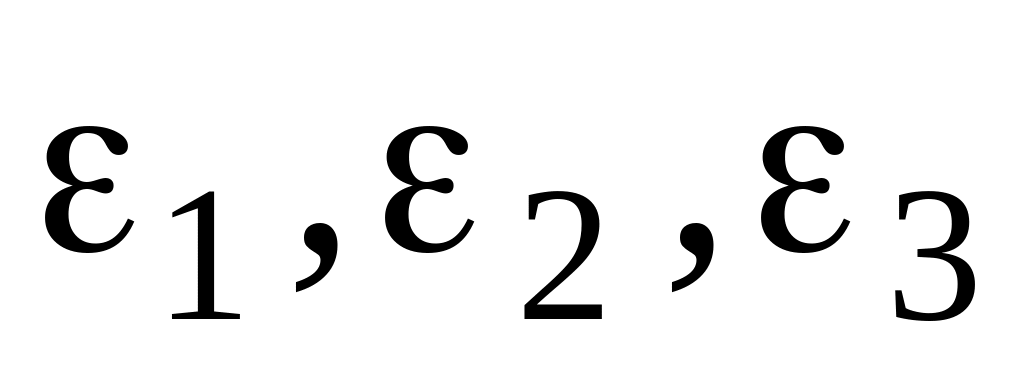4. відносну зміну об’єму;

5. питому потенціальну енергію деформації;

6. розв’язати задачу графічно, побудувавши коло напружень;

7. еквівалентне напруження та коефіцієнт запасу міцності.

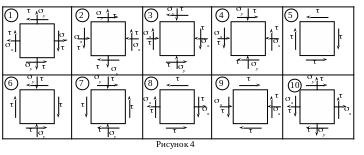Дані взяти з таблиці 4.

Таблиця 4

№ стовпця	№ схеми				Матеріал (сталь)
1	1	80	20	40	30
2	2	50	50	30	45
3	3	20	40	50	20Г
4	4	20	60	50	40Х
5	5	30	40	60	30ХГСА
6	6	40	60	80	50ХН
7	7	50	30	50	10
8	8	60	40	20	12ХН3А
9	9	60	30	40	30ХН3А
0	10	70	20	30	35ХМ
	е	г	в	б	а