Рівняння Шредінгера

1⁰. У квантовій механіці постає важлива проблема про відшукання такого рівняння, яке б мало таке саме значення, як рівняння руху Ньютона для класичної механіки. Положення частинки в квантовій механіці описується заданням псі-функції, тому рівняння має бути хвильовим.

Основне рівняння квантової механіки було знайдено у 1926 році Е.Шредінгером. Воно постулюється. Фундаментальне лінійне диференційне рівняння нерелятивістської квантової механіки, яким описується динамічний стан мікросистеми називається рівнянням Шредінгера. Його найзагальніший вигляд такий:

(7.3)

де Н – оператор Гамільтона системи, оператор повної енергії

У вужчому розумінні - це основне часове рівняння нерелятивістської динаміки мікросистеми, яка перебуває в зовнішньому полі:

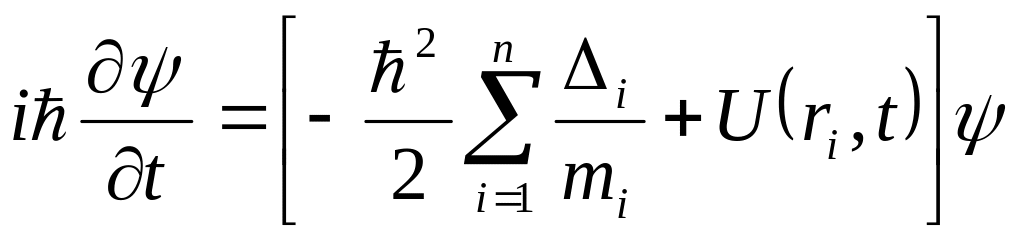, (7.4)

де – оператор Лапласа ( ), – маса і-ої частинки, , , U – потенціальна енергія нерелятивістських частинок системи.

2⁰. Важливо також знайти стаціонарні розв’язки рівняння Шредінгера, які не містять часу. Якщо потенціальна енергія U не залежить явно від часу, то стаціонарні стани описуються стаціонарним рівнянням Шредінгера:

(7.5)

де Е - повна енергія системи. Хвильова функція в цьому рівнянні є функцією координат. Окремим випадком рівняння є рівняння Шредінгера для безспінової частинки, яка міститься в певному силовому полі:

(7.6)

Для цілком вільної частинки (U = 0)

(7.7)

. Функції , які задовольняють рівнянню Шредінгера при заданому називаються власними функціями. Вони існують (при вимозі однозначності, скінченності і неперервності) лише при певних значеннях Е, які називаються власними значеннями енергії. Сукупність власних значень Е утворюють енергетичний спектр частинки. Коли U – монотонна функція і на нескінченності, то в області власні значення енергії утворюють дискретний спектр. Отже, з рівняння Шредінгера автоматично випливає квантованість основних параметрів мікросистеми. Знаходження власних значень енергії і власних функцій є задачею квантової механіки.

4⁰. Коли , часове рівняння Шредінгера має рішення:

(7.8)

Залежність стану частинки від часу t описується періодичною функцією часу з циклічною частотою , яка визначається енергією Е частинки. Ця формула відповідає зв’язку енергії частинки Е з частотою хвилі де Бройля.

Коли частинка знаходиться в енергетичному стані з , то ймовірність знайти її в елементі об’єму не залежить від часу:

Такий стан частинки називається стаціонарним станом.

Атом, який знаходиться в стаціонарному стані, має постійну енергію і не випромінює електромагнітних хвиль.

Принцип суперпозиції в квантовій механіці

1⁰. Коли вісь ОX спрямована вздовж швидкості вільної частинки ( ), то стаціонарне одновимірне рівняння Шредінгера

має такий розв’язок:

, (7.9)

де А і В – сталі величини, m – маса частинки.

Тобто, вільній частинці в квантовій механіці відповідає плоска монохроматична хвиля де Бройля.

Відомо, що загальне рівняння плоскої монохроматичної хвилі має вигляд

(7.10)

а якщо t = 0, то

. (7.11)

Порівнявши рівняння (7.9) і (7.11), дійдемо висновку, що хвильове число вільної частинки

.

Водночас хвильове число

.

Оскільки в цю формулу входить довжина хвилі де Бройля, дістаємо значення повної енергії частинки у вигляді

. (7.12)

Тобто, енергія вільної частинки може набувати будь-яких додатніх значень. Її енергетичний спектр є бесперервним. Ймовірність знайти частинку в будь-якій точці простору – величина стала. Для хвилі, яка розповсюджується в позитивному напрямку осі ОХ,

Часове рівняння Шредінгера для вільної частинки має розв’язок:

(7.13)

який є суперпозицією двох плоских монохроматичних хвиль, рівної частоти (див.(7.10) та (7.13)), які розповсюджуються одна в позитивному напрямку осі OX з амплітудою А, друга – в протилежному напрямку з амплітудою В.

2⁰. Рівняння Шредінгера не виводиться, а постулюється і відбиває хвильову природу мікрочастинок. Воно правильне, бо висновки з нього підтверджуються практикою.

§.Квантова частинка у зовнішньому стаціонарному полі. Властивості стаціонарних станів. Один із прикладів одновимірного руху квантової частинки: частинка в потенціальній ямі.

1 ⁰. Потенційною ямою називається область простору, в якій потенціальна енергія U частинки менша деякого значення . До речі, при i маємо одномірну потенціальну яму нескінченої глибини. Коли потенціальна енергія частинки

при 0<x<L,

при x<0 і x>0,

то яма має „плоске дно” (рис.8.1).

 Стаціонарне рівняння Шредінгера для частинки в потенціальній ямі має вигляд

(8.1)

при крайових умовах . Це означає, що і поза областю , тобто ймовірність знайти частинку поза потенціальною ямою дорівнює нулеві.

Розв’язок рівняння Шредінгера має такий вигляд:

, (8.2)

де А і В – сталі, – хвильове число. Звідкіля

. (8.3)

Із крайових умов випливає, що ; і , тобто хвильове число набуває таких дискретних значень: , де

Останнє рівняння означає, що

, і , (8.4)

тобто на довжині потенціальної ями повинно укладатись ціле число півхвиль де Бройля: .Отже, усередині ями утворюється стояча хвиля де Бройля або стояча електронна хвиля! На стінках ями утворюються вузли стоячої електронної хвилі (рис.8.2 а).

З виразу (8.3) і (8.4) власні значення енергії частинки в одномірній потенціальній ямі нескінченої глибини

( ) (8.5)

є дискретним рядом значень енергії, як кажуть – квантованим.

Квантовані значення називаються рівнями енергії, а числа n, які визначають енергетичні рівні частинки потенціальної ями, називаються головними квантовими числами. Енергія електрона залежить від головного квантового числа, але має однакове значення по всій довжині ями. Саме тому з’явився термін: енергетичний рівень. Найменше можливе значення енергії відповідає головному квантовому числу n = 1.

Якщо відношення . Тобто при означає, що виникає зближення енергетичних рівнів частинки в потенціальній ямі. Звідсіля випливає, що квантування енергії при великих квантових числах дає результати близькі до результатів класичної фізики – енергетичні рівні стають квазібезперервними. Це є показником слушності основ квантової механіки.

З виразу (8.2) і (8.4) знайдемо власні функції:

. (8.6)

З вимоги нормування

.

Т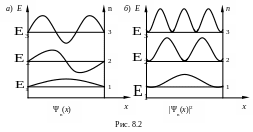 обто,

Звідки і власні функції мають вигляд:

.(8.7)

Графіки власних функцій, які відповідають рівням енергії (8.5) зображені на рис. 8.2 а). На рис. 8.2 б) зображена густина ймовірності знаходження частинки на різних відстанях від стінок ями.

Імовірність перебування електрона всередині ями визначається за формулою:

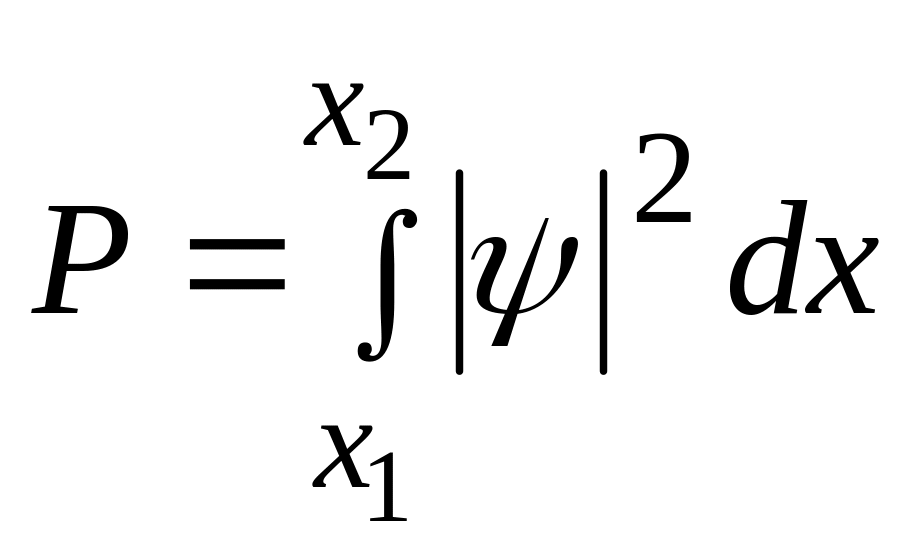. (8.8)

З малюнка випливає, що, наприклад, у квантовому стані з частинка не може знаходитися в середині „ями”. Таке поводження частинки не сумісне з поняттям траєкторії!

Дано

1s,  l1 = 0 Е = 12,1 еВ = 1,94·10-18 Дж l 2 = lmax

Визначити

§. Задача 3. 1s електрон атома водню поглинув фотон з енергією 12,1 еВ, перейшов в збуджений стан з максимально можливим орбітальним квантовим числом. Визначте зміну орбітального моменту імпульсу електрона, запишіть квантові числа збудженого стану. В якому стані знаходиться електрон?

Розв’язання: , ,

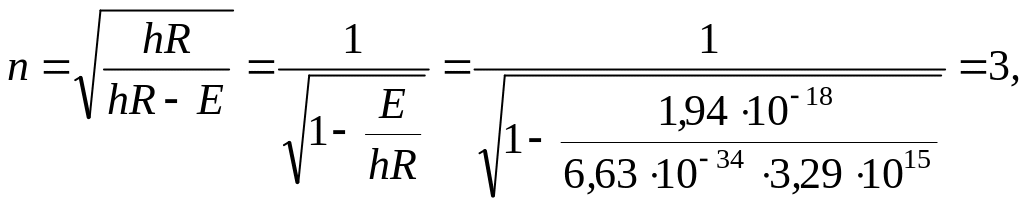
§.Протонно-нейтронний склад ядра. Ядерні сили та їх властивості. Дефект маси, енергія зв’язку ядра. Основні характеристики ядер. Властивості ядерних сил. Моделі ядра. Ядерні реакції поділу та синтезу. Ланцюгові реакції. Ядерна енергетика та екологія. Проблеми керованих термоядерних реакцій.

Ядром називається центральна частина атома, у якій зосереджена практично вся маса атома і його позитивний електричний заряд.

Основними характеристиками стабільного ядра є заряд, маса, радіус, спін, магнітний момент, парність, квадрупольний електричний момент.

Радіоактивні ядра додатково характеризуються типом радіоактивного перетворення ( _- чи _- розпад, спонтанний розподіл і ін.), періодом напіврозпаду, енергією частинок, що випускаються тощо.

Ядерна фізика вивчає будову ядра, його перетворення і взаємодію з іншими ядрами і частинками.

Всі атомні ядра складаються з елементарних частинок: протонів і нейтронів, що вважаються двома зарядовими станами однієї частинки – нуклона. Протон (р) має позитивний заряд, який дорівнює заряду електрона, і масу спокою m_p = 1,672610^-27кг. Нейтрон (n) – не має електричного заряду, маса спокою m_n = 1,674910^-27кг.

Зарядом ядра називається величина Zе, де е – заряд протона, Z – зарядове число ядра, що дорівнює числу протонів у ядрі (і, отже, кількості електронів у атомних оболонках) і співпадає з порядковим номером хімічного елемента в Періодичній системі елементів Менделєєва (Z = 1…110).

Ядро (нуклід) символічно позначають: , де Х – символ хімічного елемента, А = N + Z – масове число (число нуклонів у ядрі), N – число нейтронів.

Ядра з однаковими Z, але з різними А називаються ізотопами (існують, наприклад, три ізотопи кисню , , ).

Ядра з однаковим А, але з різним Z називаються ізобарами. Усього відомо ~300 стійких ізотопів хімічних елементів і більш 2000 природних і штучно отриманих радіоактивних ізотопів. Число можливих нуклідів оцінюється в ~4000.

Розмір ядра характеризується радіусом ядра, який можна знайти з емпіричної формули:

, (17.1)

де R₀ = (1,3...1…1,7)10^-15м. Це в 100000 разів менше радіуса атома. Густина ядерної речовини приблизно однакова для всіх ядер і складає ~10¹⁷ кг/м³ (для порівняння, густина води 10³ кг/м³).

Експериментальні дані вказують на приблизну сферичність ядра і на те, що густина заряду постійна усередині ядра (при Z>6) і плавно зменшується до нуля поблизу його границь. Мірою відхилення розподілу електричного заряду протонів по ядру від сферично симетричного є квадрупольний електричний момент ядра Q. Так, для еліпсоїда обертання з рівномірним розподілом по ньому заряду:

(17.2)

де b і а – півосі еліпсоїда.