Пересечение прямой с плоскостью
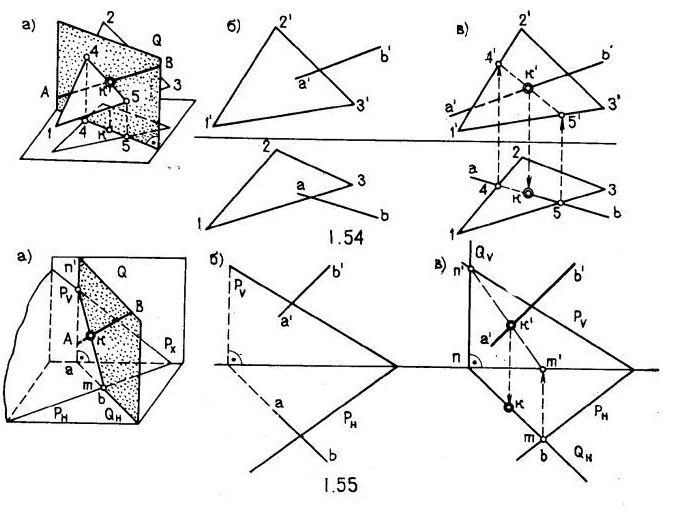
1) Плоскость задана прямыми 1 – 2 и 2 – 3 ( треугольником) (рис.1.54)
2) плоскость задана следами РН и РV (рис.1.55).
Алгоритм решения один для обоих случаев. Через АВ проводится вспомогательная горизонтально – проецирующая плоскость Q. Находится линия 4 – 5 (M, N) пересечения этой вспомогательной плоскости Q с данной плоскостью Р. Точка К пересечения полученной линии 4 – 5 (M, N) с данной прямой АВ будет точкой пересечения прямой АВ с плоскостью Р.
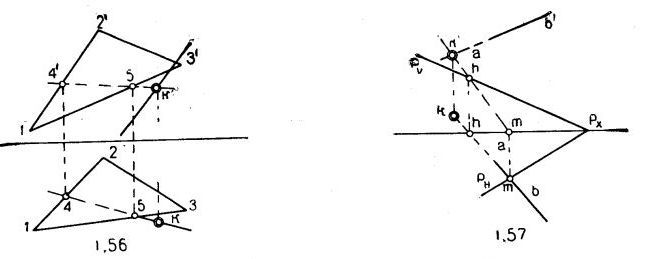
Точка пересечения К может получиться вне контура треугольника (рис.1.56). точка пересечения К (k, k') может получиться не в первой четверти (рис.1.57).
Взаимно перпендикулярные прямые и плоскости
Теорема: две плоскости взаимно перпендикулярны, если одна из них проходит через прямую перпендикулярную другой (рис.1.63).
Взаимно перпендикулярные плоскости не могут иметь обе пары одноименных следов взаимно перпендикулярными. Поэтому на рис.1.64, а плоскости Р и Q не перпендикулярны. Для другого случая (рис.1.64, б) нужно сделать попытку в одной плоскости взять прямую, перпендикулярную другой плоскости.
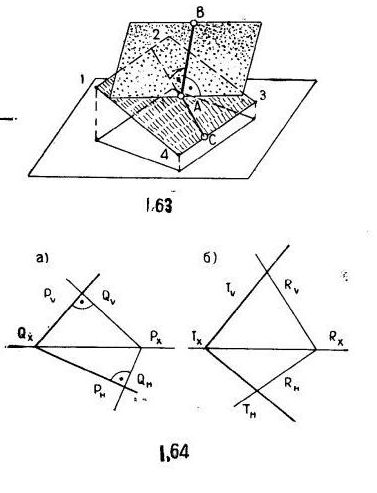
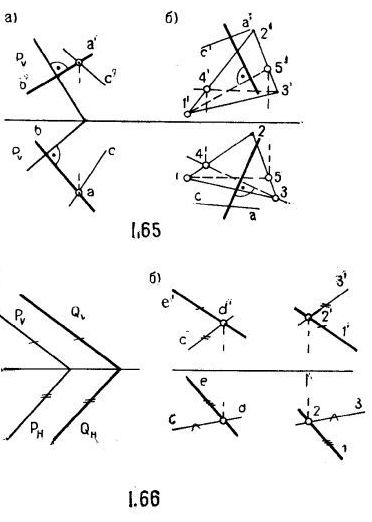
Две прямые, из которых одна АВ перпендикулярна плоскости Р (рис.1.65), определяют плоскость, перпендикулярную данной плоскости Р. На рис.1.65, а плоскость задана следами; на рис.1.65, б плоскость задана прямыми (треугольником 1 – 2 – 3).
Если параллельные плоскости заданы следами, то их одноименные следы параллельны (рис.1.66, а).
Если параллельные плоскости заданы прямыми, то любым двум пересекающимся прямым одной плоскости найдутся параллельные пересекающиеся прямые другой плоскости (рис.1.66, б).
Вопросы самоконтроля:
1) Что называют эпюрой?
2) Как называются плоскости Н, V и W?
3) Что такое прямая частного положения?
4)Что называют следами прямой линии?
5) Что такое следы плоскостей?
6)Что такое горизонталь, фронталь и линия наибольшего ската?
Способы преобразования чертежа Характеристика способов
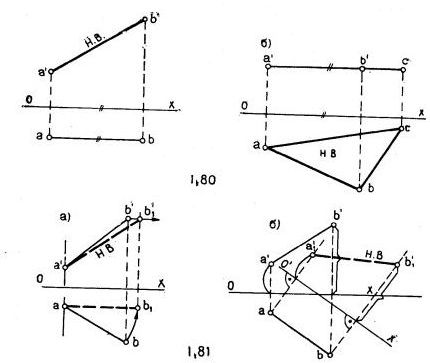
При частных положениях объекта, когда отдельные его элементы (ребра, грани) располагаются параллельно или перпендикулярно плоскости проекций, эти элементы на одной из проекций изображаются без искажений. Например, когда отрезок параллелен плоскости V, то фронтальная проекция равна его натуральной величине (рис.1.80, а) или когда плоскость треугольника параллельна плоскости Н, то горизонтальная проекция равна его натуральной величине (рис.1.80, б) и т.д.
Для перехода в проекциях от общего положения объекта к частному служат способы преобразования проекций.
Способ вращения состоит в том, что изменяется положение объекта путем вращения вокруг соответствующей оси, а плоскости проекций остаются неизменными (рис.1.81,а).
Способ перемены плоскостей проекции заключается в том, что изменяется положение плоскостей проекций, а положение объекта остается неизмененным (рис.1.81, б).
Натуральная величина отрезка найдена на рис.1.81, а способом вращения вокруг вертикальной оси. На рис.1.81, б – переменной фронтальной плоскостей проекций.
После преобразования новая проекция объекта дает возможность определить интересующую нас величину (например, угол и пр.).
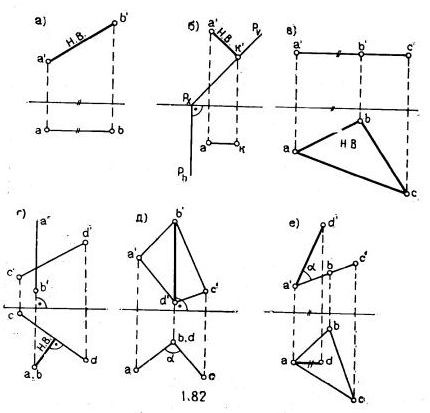
Некоторые случаи положения объектов, при которых отдельные элементы их проецируются без искажения:
а) натуральная величина отрезка, когда он параллелен плоскости проекции (рис.1.82, а).
б) величина расстояния от точки до плоскости Р, когда этот отрезок параллелен плоскости проекций (а плоскость Р перпендикулярна к той же плоскости проекций, рис.1.82, б).
в) плоская фигура, когда ее плоскость параллельна плоскости проекций (рис.1.82, в).
г) отрезок расстояния между скрещивающимися прямыми, когда одна из данных прямых занимает проецирующее положение (рис.1.82, г).
д) линейный угол двугранного угла, когда общее ребро двугранного угла, находится в проецирующем положении (рис.1.82, д).
е) линейный угол между прямой и плоскостью, когда прямая параллельна плоскости проекций, а данная плоскость перпендикулярна той же плоскости проекций (рис.1.82, е)
