Плоскость, проходящая через прямую
Для того, чтобы провести плоскость через прямую линии необходимо дополнительное условие, например требование, чтобы плоскость проходила через точку параллельно другой прямой или плоскости, и т.д.
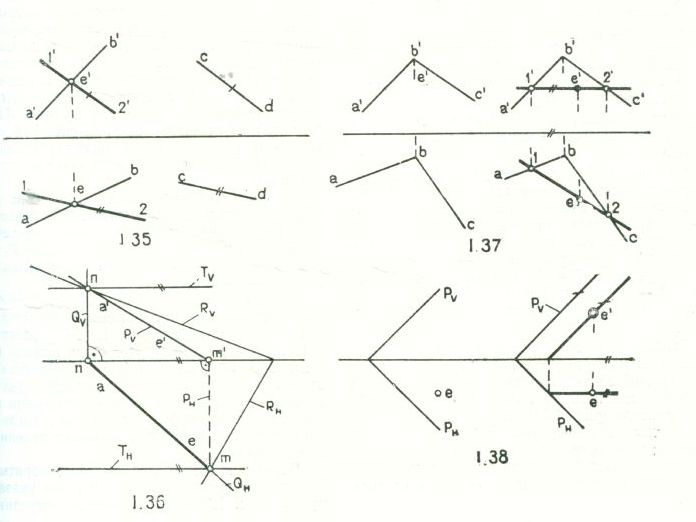
На рис.1.35 через прямую АВ проведена плоскость, параллельная прямой CD, для чего через точку Е прямой АВ проведена прямая 1-2 параллельно прямой CD.
На рис.1.36 через прямую АЕ проведены плоскости: Р – фронтально проецирующая; Q – горизонтально проецирующая; Т – параллельная оси проекций; R- общего положения. У плоскостей Р и Q один след совпадает с проекцией прямой АВ.
Чтобы взять точку Е (e'e) в плоскости, нужно взять прямую в плоскости, затем на этой прямой взять точку. Удобнее использовать горизонталь (рис.1.37) или фронталь (рис.1.38) плоскости. Если берется произвольная прямая или произвольная точка в плоскости, то одна проекция прямой или точки может быть взята произвольно, а вторая проекция должна быть определена построением.
Пересечение двух плоскостей
Основной задачей является построение пересечения двух геометрических образцов: плоскостей между собой (рис.1.39, б)- прямой с плоскостью (рис.1.39, а); плоскости и поверхности (рис.139, в); двух поверхностей (рис.1.39, г). Во всех случаях задача решается на основе одного и того же алгоритма.
Данные геометрические образы пересекаются вспомогательными плоскостями (или поверхностями), которые называются посредниками. Находятся линии пересечения посредников с каждым образом отдельно. Точки пересечения этих линий и будут принадлежать линии пересечения данных образов (рис.1.40, 1.41)
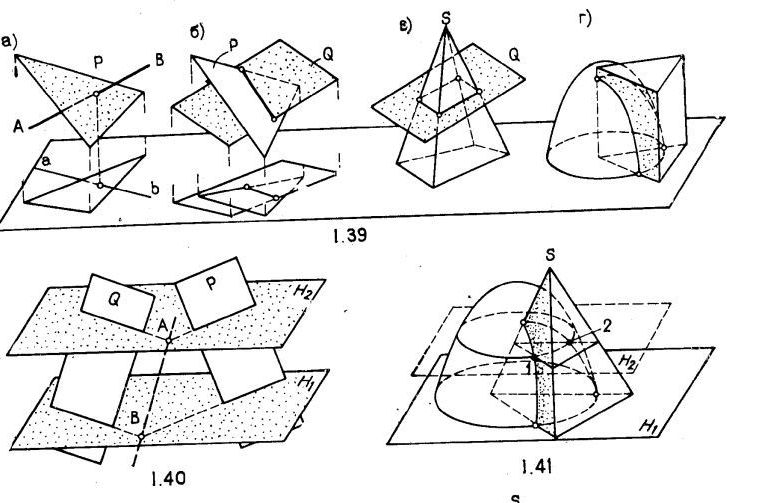
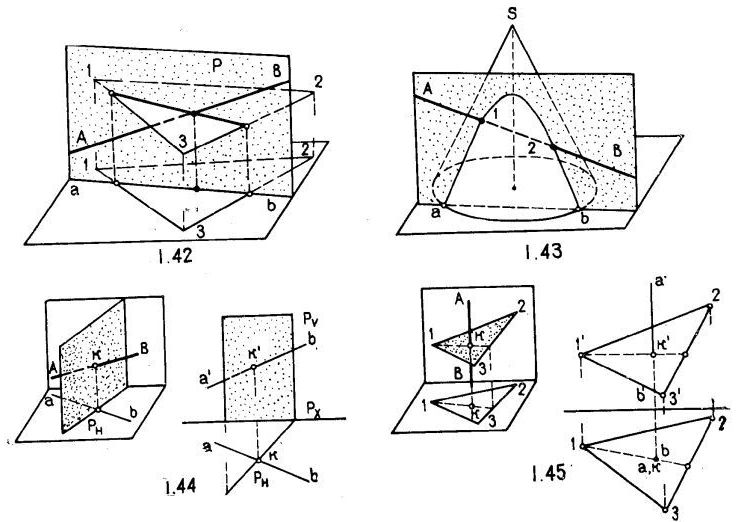
Посредники выбираются так, чтобы в пересечении с данными образцами получились простейшие линии (прямые или окружности). Посредниками преимущественно берутся плоскости уровня или проецирующие. Когда определяется точка пересечения прямой с поверхностью (или с плоскостью), посредник (плоскость) проводится через эту прямую (рис.1.42, 1.43).
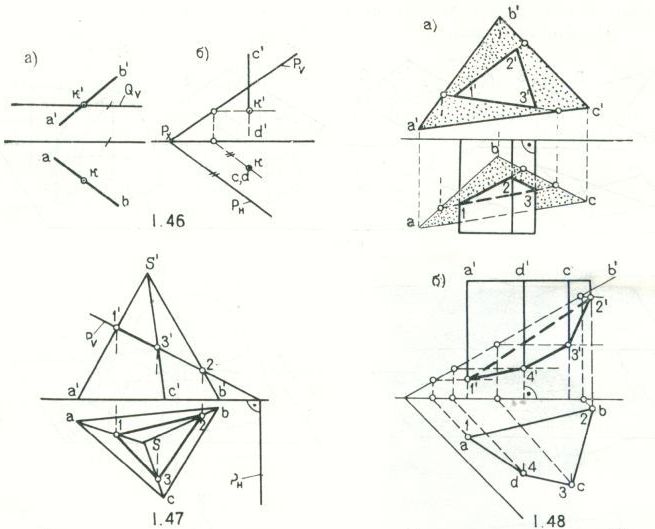
На рис.1.44 плоскость Р горизонтально проецирующая; на рис.1.45 прямая АВ горизонтально проецирующая; на рис.1.46,а плоскость Q горизонтальная (проецирующая); на рис 1.46, б прямая АD вертикальная (проецирующая).
На рис.1.47 определено пересечение пирамиды фронтально-проецирующей плоскостью, где фронтальная проекция линии пересечения 1' – 3' – 2' известна (совпадает со следом РV) и на ее основе определена и ее горизонтальная проекция 1 – 2 – 3.
На рис.1.48, а построено пересечение фронтально – проецирующих прямых плоскостей общего положения. На рис.1.48, б пример решен при помощи горизонталей.
Домашнее задание
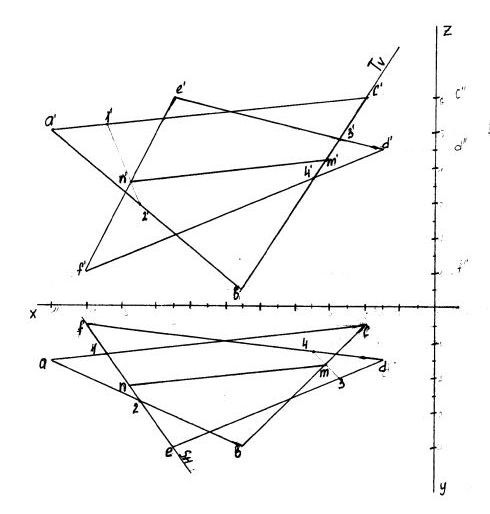
Задание: построить по заданным координатам два треугольника: АВС и DEF. Найти пересечения прямой линии mn и отобразить видимость треугольников.
А(110,15,50); В(55,40,5); С(20,5,60), D(15,15,45); Е(75,40,60), F(100,5,10)
Выполнение задания
Отложим координаты точек треугольников АВС и DEF на плоскости проекций. Стороны ef и b'c' заданы следами.
При пересечении сторон треугольников aс и ef в точке 1 находим проекцию точки на фронтальной плоскости проекций на стороне треугольника a'с' в точке 1'.
При пересечении сторон треугольников ab и ef в точке 2 находим проекцию точки на фронтальной плоскости проекций на стороне треугольника a'b' в точке 2'
Соединяем точки 1' и 2'
При пересечении 1'-2' со стороной треугольника е'f ' находим точку n'.
Из точки n' проводим проекционную связь на след ef горизонтальной плоскости. Получаем точку n.
При пересечении сторон треугольников b'c' и d'e' в точке 3' находим проекцию точки на горизонтальной плоскости проекций на стороне треугольника de в точке 3.
При пересечении сторон треугольников d'f' и b'c' в точке 4' находим проекцию точки на горизонтальной плоскости проекций на стороне треугольника df в точке 4.
Соединяем точки 3 и 4
При пересечении 3-4 со стороной треугольника bc находим точку m
Из точки m проводим проекционную связь на след b'c' фронтальной плоскости. Получаем точку m'.
Соединяем точки m и n, m' и n'.
Прямые mn и m'n' определяют видимость пересекающихся треугольников
