Прямые и точки в плоскости

Прямая принадлежит плоскости, если 2 ее точки принадлежат данной плоскости.

Среди прямых, лежащих в плоскости, есть особые, определенно расположенные, которые имеют большое значение при решении ряда задач. Эти прямые называются главными линиями плоскости. Это горизонталь плоскости, фронталь плоскости и линия наибольшего наклона плоскости ( к плоскости проекций).

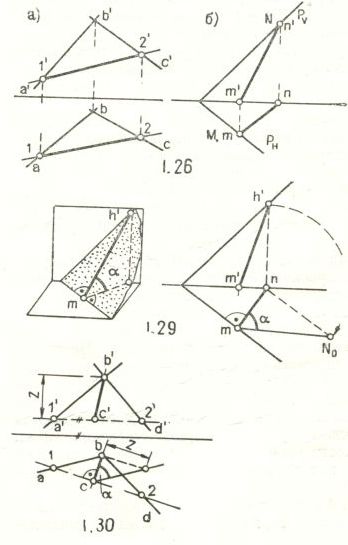
Для того, чтобы прямая лежала в плоскости, нужно, чтобы она имела с ней две общие точки ( точки 1 и 2 на рис.1.26,а). Если плоскость задана следами, то следы прямой ( лежащей в плоскости) совпадают с одноименными следами этой плоскости: М, m – с Р_Н; Nn' – с Р_V (рис.1.26,б).

На рис.1.27 изображена горизонталь плоскости n'A, горизонтальная проекция ее располагается параллельно следу Р_Н, фронтальная – параллельно ОХ.

На рис.1.28 изображена фронталь плоскости МВ; горизонтальная проекция ее располагается параллельно ОХ, фронтальная – параллельно следу Р_V.

На рис.1.29 изображена линия наибольшего наклона плоскости Р к плоскости Н.

Среди множества прямых, которые могут быть проведены в плоскости, следует выделить главные линии плоскости:

1) Горизонтали – прямые, принадлежащие плоскости и параллельные горизонтальной плоскости проекции.

2) Фронтали – прямые в плоскости параллельные фронтальной плоскости проекции. Горизонтальная проекция фронтали горизонтальна, т.е. перпендикулярна линиям связи.

3) Линии наибольшего ската (наклона) – это прямые, принадлежащие данной плоскости и перпендикулярные горизонталям или фронталям плоскости.

Построение следов плоскости

След плоскости – это линия пересечения заданной плоскости с плоскостью проекций.

Каждый след плоскости представляет собой линию для построения, которой необходимо определить две ее точки (одной из них может служить точка схода следов на оси проекции), если известно направление следа плоскости – достаточно построить одну точку к искомому следу.

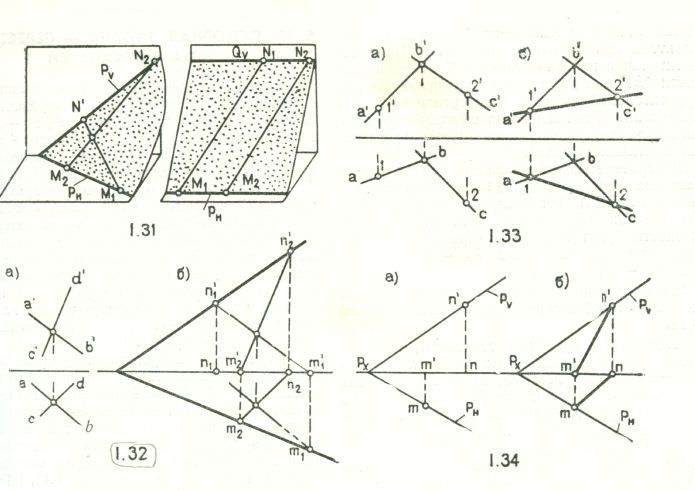
Иногда нужно построить следы плоскости, заданной двумя прямыми (рис.1.31). Тогда определяют следы данных прямых М₁М₂ – N₁N₂ (рис.1.32). Следы плоскости будут проходить через одноименные следы этих прямых: след Р_Н – через m₁m₂, след Р_V – через n'₁n'₂.

Следы плоскости должны пересекаться на оси ОХ в собственной или в несобственной точке.

Чтобы взять прямую в плоскости, заданной двумя прямыми, нужно взять на этих прямых две точки 1 и 2 (рис.1.33, а) и их соединить (рис.1.33, б). Если плоскость задана следами (рис.1.34), удобнее взять не случайные точки, а следы прямой m, m'; n, n', которые совпадают с одноименными следами плоскости.

Домашнее задание

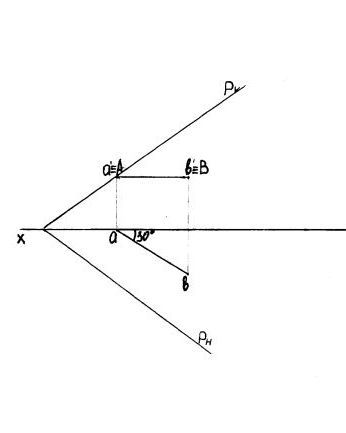
Задание : построить следы прямой АВ в плоскости Р.

Выполнение работы:

1. Прямая АВ лежит на фронтальной плоскости

2. Она совпадает с прямой АВ в фронтальных проекциях a'b'.

3. На горизонтальной плоскости находим след ab

4. Проекция точки А на горизонтальной плоскости проекций лежит на оси х.

5. аb ^ х = 30º ( ^ - угол)