Две линии ( взаимные положения прямых)

Прямые линии в пространстве могут быть параллельными, скрещивающимися, пересекающимися.

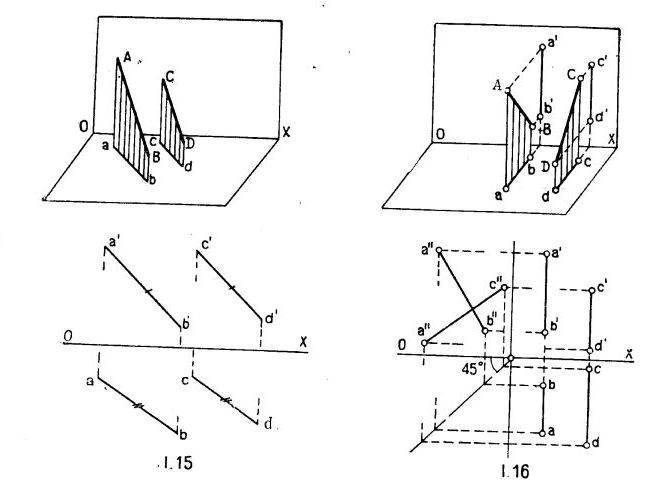
1) Параллельные линии - Одноименные проекции параллельных прямых параллельны (рис.1.15)

Для определения параллельности профильных прямых необходимо построить их профильную проекцию ( рис.1.16).

2) Пересекающиеся прямые – одноименные проекции пересекающихся прямых пересекаются, и точки их пересечения находятся на одной линии связи ( рис.1.17). Пересекающиеся прямые образуют угол ( острый или тупой), который проецируется без искажений только тогда, когда его плоскость параллельна плоскости проекции.

Если две прямые пересекаются под прямым углом, то в общем случае их проекции образуют угол не равный 90º. Прямой угол проецируется в истинную величину, если одна из его сторон параллельна плоскости проекции.

3) Скрещивающиеся прямые – одноименные проекции скрещивающихся прямых, но точки их пересечения не лежат на одной линии связи ( рис.1.18)

Точки, принадлежащие скрещивающимся прямым и лежащие на общем проецирующем луче, называются конкурирующими ( точки 1, 2 и 3,4 ).

Домашнее задание

Построить проекции прямых в пространстве по заданию преподавателя.

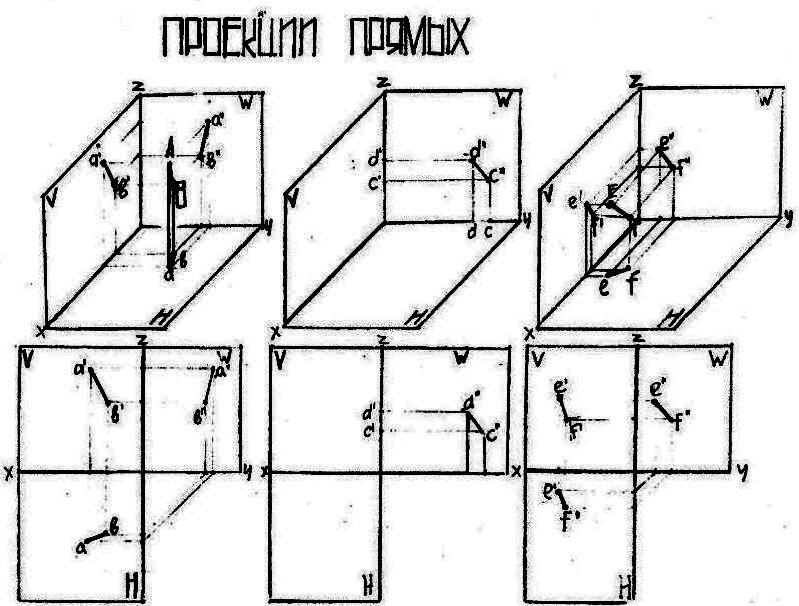
Задание: построить проекции прямых АВ, DC и EF и найти их следы . А(16,20,30); В(11,16,20); С(0,30,12), D(0,25,18), Е(20,6,20), F(19,10,14).

Выполнение работы:

1. Отложим на осях координаты точки А. Находим ее в пространстве.

2. Аналогично находим точку В.

3. При соединении точек А и В получаем прямую АВ.

4. При соединении горизонтальных проекций точек a и b получаем след прямой АВ на плоскости Н.

5. При соединении фронтальных проекций точек a ' и b' получаем след прямой АВ на плоскости V.

6. При соединении профильных проекций точек а'' и b'' получаем след прямой АВ на плоскости W.

7. На комплексном чертеже (эпюре) находим координаты прямой АВ.

8. Аналогично находим прямые DC и EF

Плоскость

Положение плоскости в пространстве можно определить:

а) 3-мя точками, не лежащими на одной прямой;

б) прямой и точкой вне ее;

в) 2-мя параллельными или пересекающимися прямыми;

г) любой плоскостной фигурой.

Плоскость может быть так же задана следами.

Следами плоскости называются линии пересечения плоскости с плоскостями проекций.

В общем случае плоскость имеет 3 следа: Р_Н –горизонтальный, Р_V – фронтальный, Р_W – профильный. Следы плоскости пересекаются на осях и будут обозначаться Р_Х, Р_У, Р_Z. Эти точки называются точками схода следов плоскости.

В зависимости от того, какое положение занимают плоскости, относительно плоскостей проекции, можно выделить:

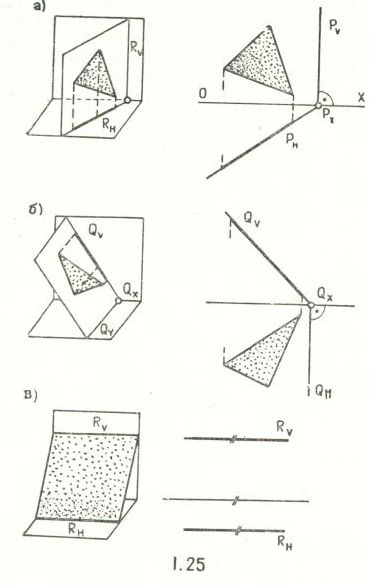
1) Плоскость общего положения – не параллельна, не перпендикулярна плоскостям проекции

2) Плоскости уровня - проецирующая плоскости параллельна плоскостям проекции

( рис.1.24)

3) Плоскости проецирующие - перпендикулярны плоскостям проекции ( рис.1.25)

Плоскости уровня и проецирующие плоскости называются плоскостями частного приложения.