Домашнее задание

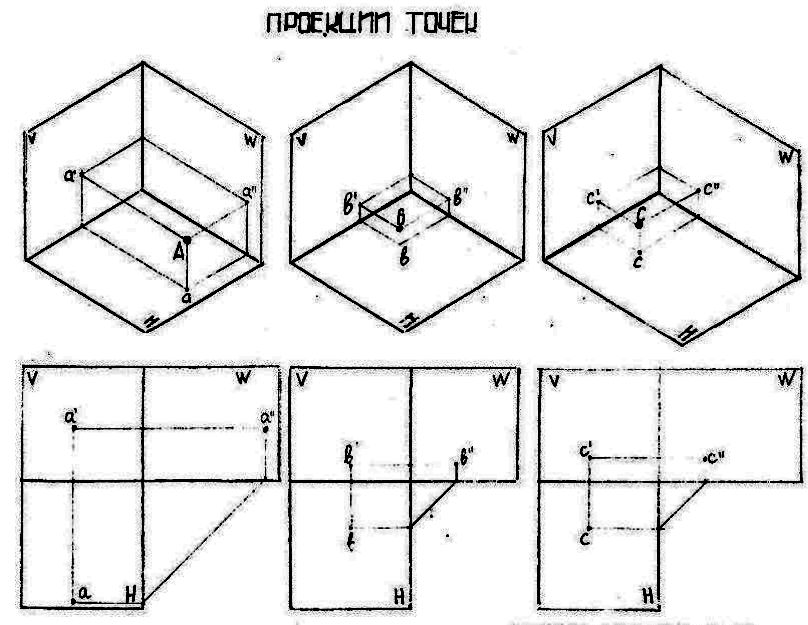
Построить проекции точек в трехгранном углу по заданию преподавателя.

Задание: построить проекции точек А(20,35,15), В(17,13,5) и С(20,13,7).

Выполнение работы:

1. Отложить на оси х 20 мм

2. На оси y – 35 мм

3. Получаем а – проекцию точки А на плоскости Н, при пересечении линий проекционных связей.

4. На оси z откладываем 15 мм.

5. Строим линии проекционных связей, параллельные осям х и y.

6. При их пересечении получаем точку А (в пространстве).

7. На комплексном (эпюре) чертеже построим проекции точки А.

8. Таким же способом строятся точки В и С.

Прямая линия

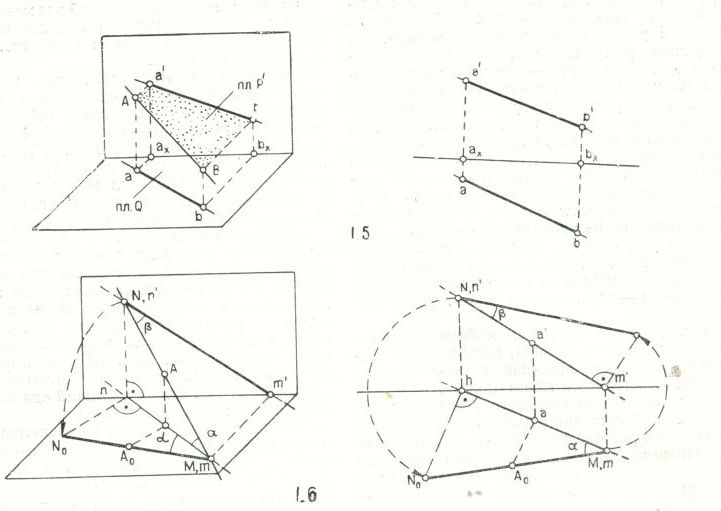
Положение прямой в пространстве определяется двумя ее точками. На изображении она будет определяться проекциями двух точек А ( а, а'); В ( b, b'), что дает две проекции прямой ab; а' b'. (рис.1.5)

Линии, проецирующие все точки прямой на плоскости Н и V, образуют плоскости Q и P, перпендикулярные Н и V и дающие в пересечении с Н и V две проекции прямой АВ.

Если точка совпадает с прямой, то проекции точки совпадают с одноименными проекциями этой прямой (рис.1.6). Если точка принадлежит отрезку, то проекция точки делит проекцию отрезка в том же отношении, в каком точка делит отрезок.

На рис.1.6 дана прямая общего положения.

Прямая общего положения: не параллельна ни одной из плоскостей проекции.

Прямая частного положения: параллельны или перпендикулярны плоскостям проекции.

Следы прямой линии

Следами прямой называются точки пересечения прямой с плоскостями проекции. Для того, чтобы на эпюре определить горизонтальный след прямой необходимо продолжить ее фронтальную проекцию до пересечения с осью О_х. И в этой точке поставить перпендикуляр до пересечения с горизонтальной проекцией прямой.

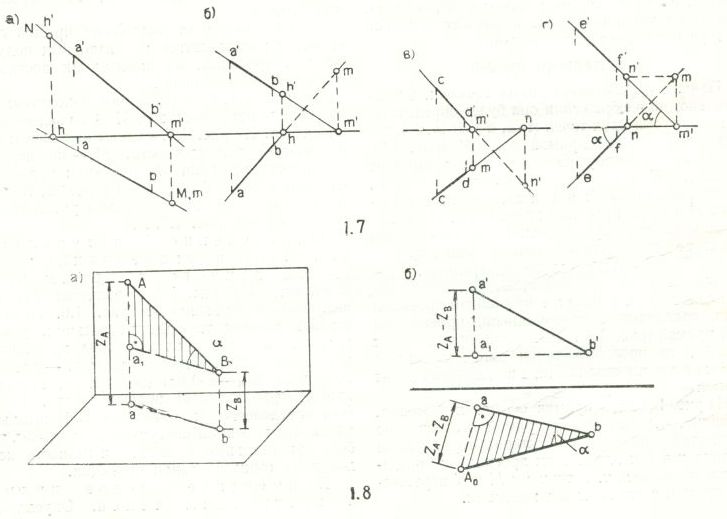
На рис.1.7,б следы прямой находятся: N – на верхней полуплоскости; М – на задней полуплоскости. На рис.1.7,в следы находятся : N – на нижней полуплоскости, М – на передней полуплоскости. Если обе проекции прямой наклонены к оси ОХ под одним углом α, то следы М и N располагаются на одном расстоянии от оси проекций (рис.1.7,г).

Решение рис.1.8,а аналогично решению на рис.1.6. Нужно построить вспомогательный треугольник, у которого одним катетом служит одна проекция ab (горизонтальная), а другим катетом – разность координат (Z_A – Z_B) концов отрезка, взятая из другой (фронтальной) проекции (рис.1.8,б).

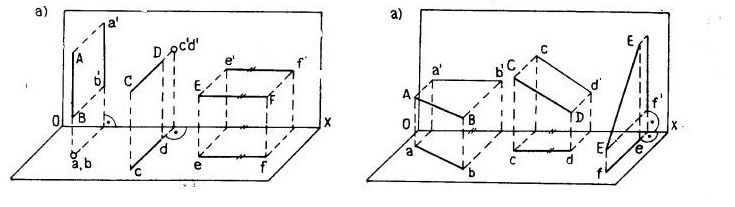
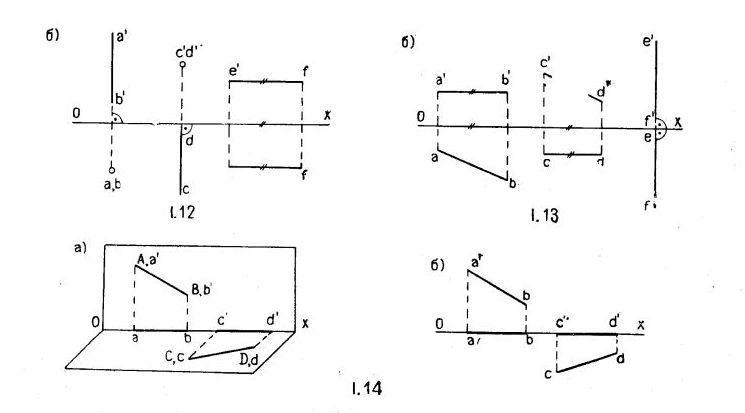
Прямые, перпендикулярные плоскости проекции, называют линиями уровня.

Прямые, параллельные плоскостям проекций, называются прямыми уровня (рис.1.13).

Прямая АВ параллельная горизонтальной плоскости проекции называется горизонталью. Она проецируется на эту плоскость поверхности в натуральную величину. Опликаты ( высоты) ее точек одинаковы, поэтому фронтальная проекция параллельна оси х.

Прямая СD параллельна фронтальной плоскости проекции и называется фронталью.

Прямая ЕF параллельна профильной плоскости проекции и называется профильной прямой.

Прямые, перпендикулярные плоскости проекции, называются проецирующими (рис.1.12).

Прямая АВ перпендикулярная горизонтальной плоскости проекции и проецируется на эту плоскость в точку называется горизонтально – проецирующей .

Прямая СD перпендикулярна плоскости проекции называется фронтально - проецирующей, а прямая ЕF – профильно - проецирующей.

Если прямая совпадает с плоскостью проекции, то одна проекция ее совпадает с осью проекции (рис.1.14).