Ортогональные проекции

Ортогональная система двух и трех плоскостей проекции: сущность метода заключается в том, что объект проецируется на 2 или 3 взаимно перпендикулярные плоскости.

Каждая из плоскостей имеет свое название:

Н – горизонтальная плоскость проекции

V – фронтальная плоскость поверхности

W – профильная плоскость проекции

Система 3-х плоскостей состоит из 8 четырехгранных углов, которые называют октантами. Линии пересечения плоскостей проекций называют осями проекции или координатными осями. И обозначают О_х, О_у, О_z .

После совмещения в одну плоскость вокруг осей проекции, полученную систему ортогональных проекций называют эпюрой.

Комплексный чертеж – чертеж трех плоскостей проекций, совмещенных в одну и содержащий три проекции точки.

Точка

Суть метода ортогонального проецирования и ортогональной проекции точки, называют – основанием перпендикуляра, опущенного из этой точки на эту плоскость.

В трехмерном пространстве положение точки определяют с помощью прямоугольных координат х, у, z.

Координаты х называются абсциссой; у – ординатой, z – аппликатой.

Прямые линии, соединяющие проекции точки, называют линиями проекционной связи.

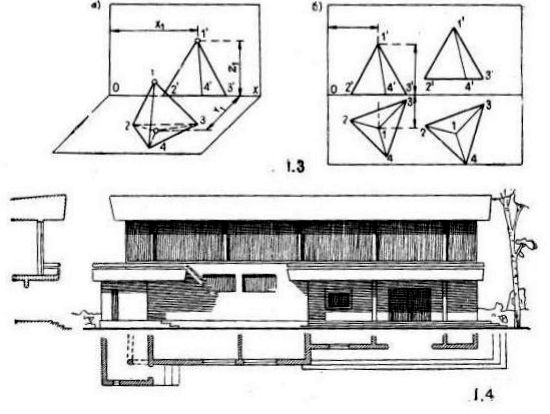
Для получения изображений объекта по методу ортогонального проецирования за плоскости проекций принимаются три взаимно перпендикулярные плоскости Н, V и W (рис.1.1). Объект ( точка) проецируется на эти плоскости перпендикулярными к ним прямыми Аа, Аа', Аа''. Точки пересечения этих прямых с плоскостям проекций а, а', а'' называются проекциями (или изображениями точки А).

Плоскости Н, V, W называются плоскостями проекций; Н – горизонтальной; V – фронтальной; W – профильной. Полученные проекции точки называются : а – горизонтальной (или планом); а' – фронтальной (или фасадом); а'' –профильной (или боковым видом).

Прямая ОХ называется осью проекции (осями проекций называются и прямые ОY, ОZ – пересечения плоскостей проекций).

Прямые Аа, Аа', Аа'' называются проецирующими.

Для получения плоского чертежа предполагается, что плоскости Н и W совмещаются с плоскостью V ( эпюра).

Координаты точки записывают А (x,y,z), например А(2,4,6).

Плоскость, образованная прямыми Аа, Аа', будет перпендикулярна плоскостям Н и V и к линии их пересечения ОХ. Поэтому линии а'а_х и аа_х на эпюре дадут одну прямую, перпендикулярную оси проекций ОХ. Эта линия называется вертикальной линией связи. Две проекции одной точки располагаются на линии связи. Третья проекция а'' точки на плоскости W строится по двум координатам z и y, величины которых известны на плоскостях Н и V. В построении используется линия, проведенная от точки О под углом 45° (рис.1.1, б), которая делит пополам угол между горизонтальной аа_y и вертикальной а''а_y линиями связи ( биссектриса связи).

Координаты точек, совпадающих с плоскостями проекций Н или V, равны нулю и соответствующие проекции их совпадают с осью проекции (рис.1.2).

Плоскости проекций могут перемещаться параллельно себе; это перемещение не отразится на изображении объекта (рис.1.3).

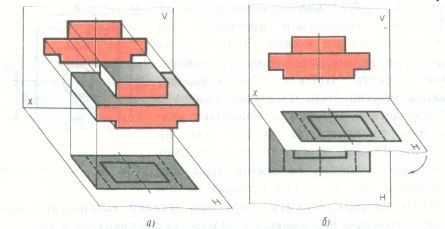
Исходя из специфических особенностей архитектурного проектирования, расположение профильной плоскости проекции W берется слева (рис.1.4).

При композиции фасадного решения проектируемого объекта внизу вычерчивают горизонтальный разрез фасадной стены со всеми конструктивными характеристиками (ленточка плана), а схему разреза этой же стены с уровнями конструктивных элементов (перекрытий, проемов), т.е. проекцию на плоскость W – слева.