Построение теней при рассеянном свете

При диффузном, рассеянном свете, проникающем через оконный проем, излучение света происходит со всей площади проема. Контуры теней как бы налагаются один на другой, их границы оказываются все более «размытыми» по мере удаления от светопроема. Плоскости откосов освещены, поэтому вертикальные и горизонтальные ребра откосов проема, обращенные внутрь помещения, являются тенеобразующими. Из множества «светящихся» точек в проеме выделяют точки, расположенные в углах проема. С помощью точе 1, 2 и 3 строят падающие тени на полу, а с помощью точек 4 и 5 – на потолке. Для построения теней необходимо спроецировать эти точки на те плоскости помещения, на которых должны быть построены тени: на пол (точки 1,2), на потолок и боковую стену (5). Затем проводят из «светящихся» точек перспективы лучевых прямых через тенеобразующие точки объекта до пересечения с вторичными проекциями лучей. Так, например, из точки 1 проведены лучи 1А и 1В через углы стола до пересечения с горизонтальной проекцией 1А₁. Аналогичным образом построена вторая тень А₀В₀ на полу от того же ребра крышки стола с помощью: лучевых прямых, проведенных через «светящуюся» точку 3(3). Для построения теней на потолке проводят лучевую прямую из точки 4 или 5 и т.д.

Тени на полу и потолке помещения не будут однородными по тону. Участки тени образуют теневые зоны «размывания» тени (полутень).

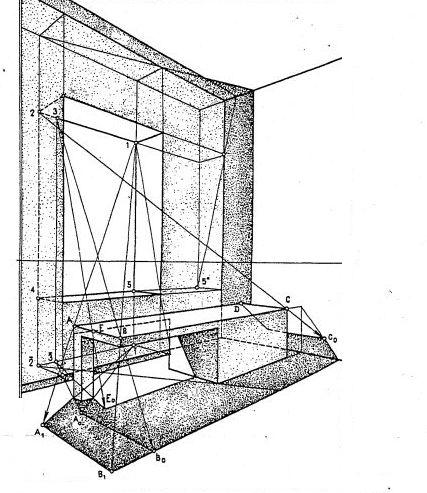
Пример : построение теней при точечном источнике света

Как и в предыдущем случае, при точечном источнике света лучевые прямые не параллельны между собой и не имеют точек схода, они пересекаются в «светящейся» точке – в точке источника света. Падающие тени строят с помощью вторичной проекции 1 светового луча, поэтому следует построить сначала проекции источника света L на те ограждающие плоскости интерьера, на которые будет нужно строить тени.

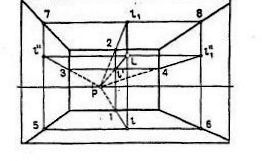
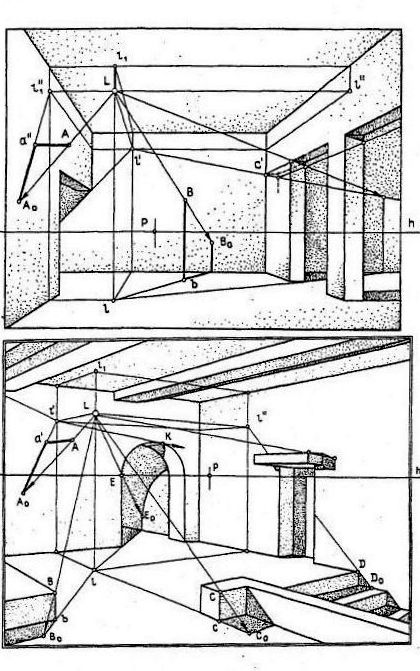
Домашнее задание

Задание: построить перспективное изображение интерьера

Выполнение задания:

1. Выбрать точку зрения.

2. Выбрать картинную плоскость и определить точку Р

3. Проводим перпендикуляр из точки Р до линии уровня глаз. Он совпадает с точкой схода всех лучей S

4. Перспектива элементов интерьера выполняется аналогично построению перспективы с одной точкой схода.

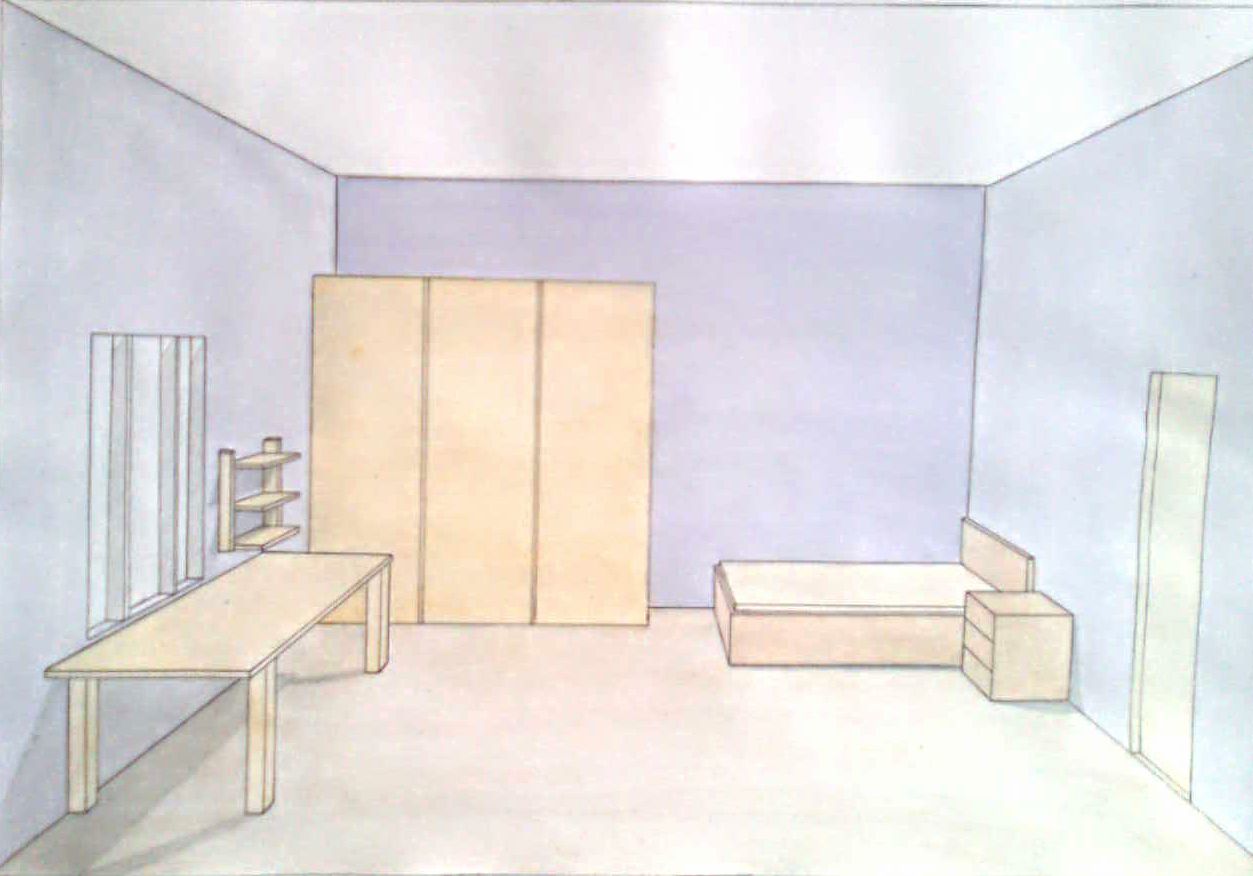
Вопросы самоконтроля:

1. Что называют фронтальной перспективой интерьера?

2. Какие существуют случай построения теней.

Список литературы:

1. «Начертательная геометрия», А.Г.Климухин. г.Москва, 1973

2. Черчение, А.Д.Ботвинников, 1997

3. Аксонометрия, Е.А.Глазунов, 1954

4. «Высшая школа», начертательная геометрия, А.М.Тевлин, 1963

5. «Построение широкоугольной перспективы с высоким горизонтом», Н.С. Кузнецов, 1958

6. Курс начертательной геометрии, А.И. Добряков, 1949

7. Начертательная геометрия, Ю.И. Короев, Москва, 2007

114