Вопросы самоконтроля:
1) В чем заключается способ перемены плоскостей.
2) Что представляет собой способ вспомогательной проекции.
Многогранники Общие сведенья. Виды многогранников.
Многогранной поверхностью называется поверхность, образованная частями (отсеками) пересекающихся плоскостей.
Многогранником называется тело, ограниченное многогранной поверхностью, состоящей из плоских многоугольников. Отсеки плоскостей называются гранями, а линии их пересечения – ребрами, точки пересечения ребер – вершинами.
Теорема: у всякого выпуклого многоугольника число граней + число вершин – число ребер = 2.
Кромке правильных выпуклых многоугольников существует большое число полуправильных многоугольников, в том числе выпукло-вогнутые (звездчатые).
Правильные многогранники
Наименование и форма |
Грани |
Верины |
Ребра |
Тетраэдр
|
4 |
4 |
6 |
Гексаэдр
|
6 |
8 |
12 |
Октаэдр
|
8 |
6 |
12 |
Додекаэдр
|
12 |
20 |
30 |
Икосаэдр
|
20 |
12 |
30 |
Области применения многогранников
В архитектурных формах соборов
В египетских пирамидах
В огранке алмазов
Вопросы самоконтроля:
1) Что называют многогранниками?
2) Какие виды многогранников существуют.
Аксонометрия
Аксонометрическими проекциями называют наглядные изображения объекта, получаемые параллельным проецированием его на одну плоскость проекций, вместе с осями прямоугольных координат, к которым этот объект отнесен.
Основная теорема Польке (по имени доказавшего ее немецкого геометра XIXв. Карла Польке): три произвольно выбранных отрезка на плоскости, выходящие из одной точки, могут быть приняты за параллельную проекцию трех равных и взаимно перпендикулярных отрезков, выходящих из некоторой точки пространства.
При построении аксонометрического изображения в соответствии с показателями искажения, приходится вычислять сокращенные размеры параметров объекта. Процесс построения упрощается, если его выполнять в приведенных в показателях искажениях. При том наибольший искажатель изображения приводят к 1.
При построении аксонометрических проекций нужно знать, как задать на плоскости Н аксонометрические оси и аксонометрические масштабные единицы.
Если направление проецирования S на перпендикулярно картине Н, то аксонометрию называют косоугольной.
Если направление проецирования перпендикулярно Н, то аксонометрия называется прямоугольной.
В косоугольной аксонометрии показатель искажения меняется от 0 до бесконечности.
∞ ≥ k ≥ 0. Случаи, когда k=0 (если S направлено вдоль оси) и k=∞ (если S || Н) является выраженным, так как k=0 у предмета не отображается третье измерение, а при k=∞ - изображения вообще нет (оно лишь теоретически- в бесконечности).
В зависимости от соотношений между аксонометрическими масштабными единицами (или коэффициентами искажения по осям) различают:
1) Триметрические проекции, когда все коэффициенты искажения различны kх ≠ kу; kу ≠ kz; kх ≠ kz.
2) Диметрические проекции, когда взаимно равны два коэффициента искажения : а)kх ≠ kу ≠ kz; б) kу = kz = kх.
В зависимости от направления проецирования аксонометрическая проекция называется прямоугольной (и косоугольной), если направление проецирования S перпендикулярно плоскости проекции и косоугольной, если направление проецирования не перпендикулярно плоскости проекции.
Классификация аксонометрических проекций:
Аксонометрия
Прямоугольная Косоугольная
Изометрия Диметрия Триметрия
Если направление проецирования S на перпендикулярно картине Н, то аксонометрию называют косоугольной.
Если направление проецирования перпендикулярно Н, то аксонометрия называется прямоугольной.
В косоугольной аксонометрии показатель искажения меняется от 0 до бесконечности.
Виды. Построение аксонометрии
1) Прямоугольная изометрия
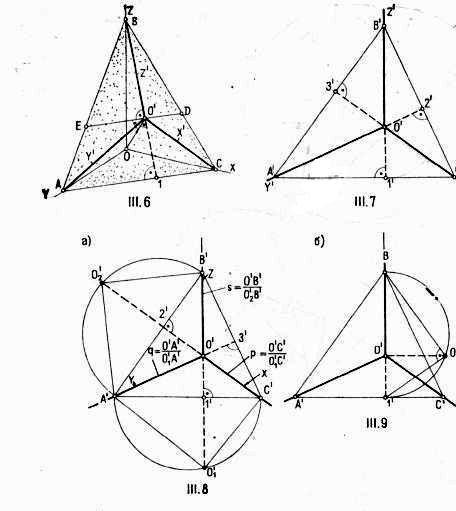
В прямоугольной изометрии углы между осями (120°), так и показатели искажения (0,82) равны (рис.111.6. – 111.12, 111.16).
2) Прямоугольная диметрия
В прямоугольной диметрии ось Y' располагается (к горизонтальной прямой) под углом 41°; ось Х' – под углом 7°. Показатели по осям Х' и Z' равны 0,94; по оси Y' – 0,47 (рис.111.13 – 111.15,111.17).
Для удобства выполнения изображения можно принять приведенные показатели, т.е. в изометрии 0,82 взять 1; в диметрии вместо 0, 94 – также 1, а вместо 0,47 – 0,5.
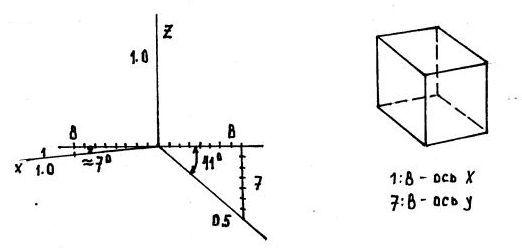
3) Фронтальная изометрия
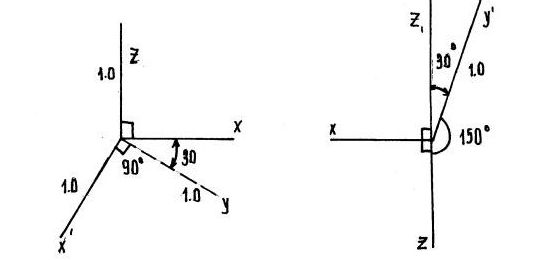
Показатели искажения равны 1.0, можно использовать по оси y = 0,5. Положение оси – под углом 45° (рис.111.19).
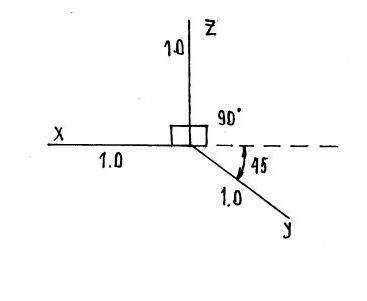
4) Фронтальная диметрия
Показатели искажения равны 1.0, можно использовать по оси y = 0,5.
5) Горизонтальная изометрия
Показатели искажения равны 1.0. Положение оси под углом 30°.
